Mathematical notation you need for A-level

Much of the mathematical notation that you need to know for A-level, you’ll already have come across at GCSE, but there are some symbols that you may not be familiar with and others that you certainly won’t have used before studying Maths at A-level.

You can find an exhaustive list in the appendices to the specification published by your exam board – Edexcel (9MA0), AQA (7357), OCR (H240) and OCR/MEI (H640) – but I’m going to provide a little more explanation for the ones that you’re most likely to come across.

The images used here are taken from the Edexcel spec, but the list is the same for all.

This article covers set notation and miscellaneous symbols that don’t fit into any other category. Here are links for other parts:
Part 2: Other Pure Maths notation
Part 3: Vectors, Statistics and Mechanics

Set notation

It’s likely that you’ll have come across some set notation at GCSE, such as the union and intersect symbols, and listing the members of a set enclosed in curly brackets, but there are more symbols you need to understand.

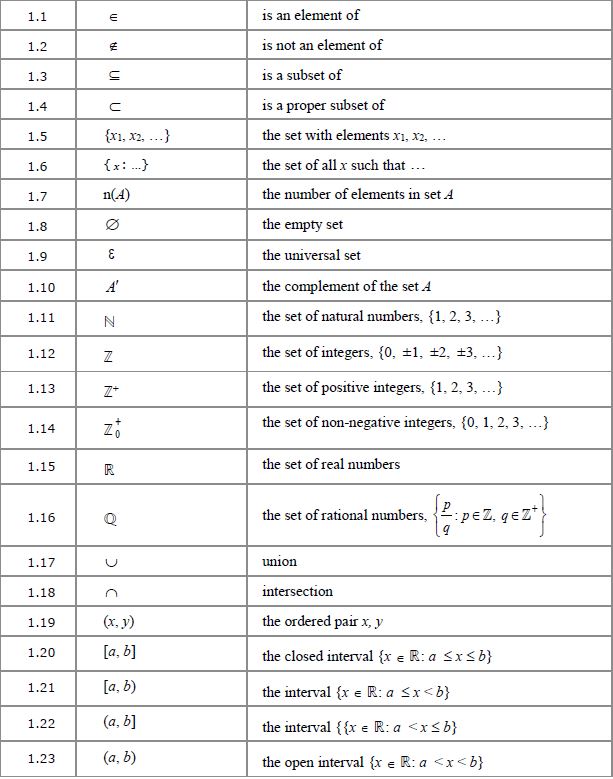
1.1 to 1.4 and 1.11 to 1.15 Number types and relationships

Let’s start with the mathematical notation for different number types.

is the set of real numbers – in other words any number that doesn’t involve the square root of a negative value. This covers all the numbers that you’ll be dealing with in A-level Maths. If you study Further Maths at A-level then you’ll also be dealing with imaginary numbers (where the imaginary number ), but you don’t need to worry about those for the single A-level.

is the set of rational numbers: numbers that can be written as a ratio or fraction, i.e. one value divided by another. Think of it as Q for Quotient; the quotient is what you get when you divide one value by another. For example, is a rational number sometimes used as an approximation for π, which is irrational.

is the set of integers, i.e. whole numbers, including zero and negative integers. It can be modified by adding a superscript “+” to specify the inclusion of only positive values, and a subscript “0” to include 0 as well.

is the set of natural numbers, i.e. the numbers that you count with. This is exactly the same as the set of positive integers, .
(Some definitions of include zero but the English A-level doesn’t.)

We can use the symbols 1.1 to 1.4 to show the relationships between the sets. For example:

– the set of integers is a proper subset of the set of real numbers, i.e. all integers are real, but not all real numbers are integers.

It could also be said that : All natural numbers are positive integers. In fact it also goes the other way – all positive integers are natural numbers – so you could just use instead of .

The relationship between and is equivalent to the relationship between the exclusive inequality and the inclusive one .

And the symbol indicates membership of a set: but , i.e. 4.7 is a rational number (it can be written as, for example, ) but not an integer.

1.6 to 1.8 Answers using set notation

If you’re asked to give the answer to an inequality question using set notation then this is the form of mathematical notation that you should use. Let’s say you’ve solved your inequality and found that has to be greater than 2 and less than or equal to 7. You’d normally write this solution as but in set notation it would look like this:

which alternatively could be written using the (intersect or AND) symbol as

It’s implied that is a real number, so you can usually omit , but if it has to be an integer then you should include that too:

On the other hand, if had to be either less than or equal to 2, or greater than 7 (and of course couldn’t be both at the same time), then you’d use the (union or OR) symbol and write
.

1.20 to 1.23 Inclusive and exclusive inequalities

Finally (for this section) we have an alternative form of mathematical notation used to indicate inclusive and exclusive inequalities. A round bracket indicates an exclusive inequality and a square one is inclusive.

So is an alternative way of writing , meaning that can take any value from 2 to 7, including 7 but not including 2.

You sometimes see this notation used in mark schemes to indicate what range of answers is acceptable, so although you’re not required to use it yourself, it can be useful to know what it means!

Miscellaneous symbols

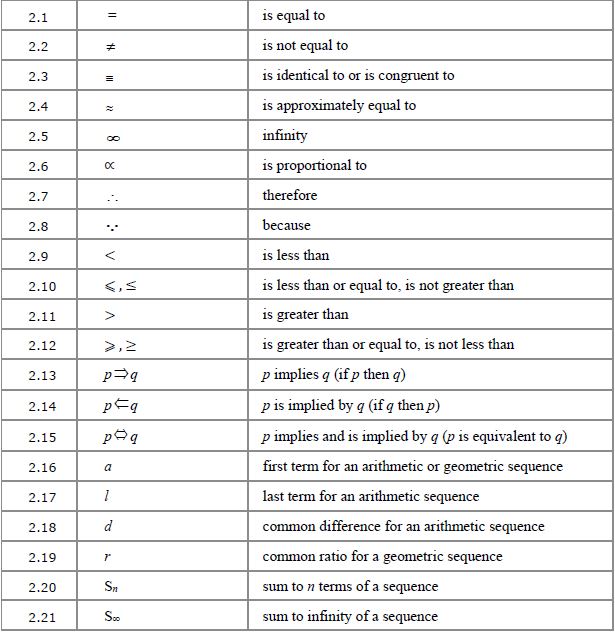
2.1 to 2.4 Equivalence

The main difference between and is that can be used where a relationship is true only for certain values of the variables, whereas indicates that two expressions are just different ways of writing the same thing, regardless of the values of any variables involved. This is the definition of an identity, which is a word you should be familiar with from GCSE.

So it would not be appropriate to use the symbol in because the expression is only true when the value of is 3.
However, – you can use the symbol here because is the same as no matter what the value of is.

2.7 to 2.8 and 2.13 to 2.15: Therefore, because and implies

The mathematical symbols for “therefore” ( ) and “implies” ( ) are very useful in writing out proofs. These two symbols are usually interchangeable, and are used in the case where, if A is true, then B must be true. For example:

or

Equally, you could say that BECAUSE :

However, note that it doesn’t go the other way: if then that doesn’t necessarily mean that ; you could also have got by squaring .

On the other hand,

or

is also true going in the other direction – if x = 3 then x + 5 will always be 8 – so the “implies” arrow could point in both directions:

Which way(s) should the “implies” arrow go in each of these cases?

1. 
2. The shape is a square The shape is a rectangle
3. 
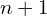4. is odd 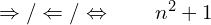is odd

Answers:

1. Both ways; 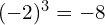and
2. To the right; all squares are rectangles but not all rectangles are squares
3. To the left; if 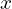is an integer then you’ll get another integer when you square it, but 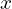will only be an integer if is a square number. Not all integers have integers as their square roots.
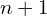4. Both ways; If is odd then 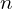must be even, therefore 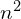must be even and so 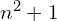is odd.
   Similarly, if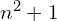 is odd then 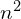is even, which means it must have a repeated factor of 2, so its square root must also have a factor of 2, i.e. must be even, and so 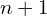must be odd.

One more symbol that isn’t listed, but that you may encounter in text books or online examples not specifically aimed at this particular qualification, is , which means “for all”. For example, means “for all integer values of “.

That’s all for this article. You can find the next one (covering most of the remaining mathematical notation for Pure Maths) here, and the one covering Vectors, Statistics and Mechanics here.