Much of the mathematical notation that you need to know for A-level, you’ll already have come across at GCSE, but there are some symbols that you may not be familiar with and others that you certainly won’t have used before studying Maths at A-level.

My last blog post covered set notation and miscellaneous symbols that don’t fit into any other category. This one, part 2, covers the other categories of mathematical notation for Pure Maths. Vectors and the mathematical notation used for Statistics and Mechanics can be found in part 3, here.

You can find an exhaustive list in the appendices to the specification published by your exam board – Edexcel (9MA0), AQA (7357), OCR (H240) and OCR/MEI (H640) – but I’m going to provide a little more explanation for the ones that you’re most likely to come across.

The images used here are taken from the Edexcel spec, but the list is the same for all.

Operations

Some of these symbols you’ll have been familiar with since early in primary school, but others – some of them meaning the same things – will be new to you.

3.3 Multiplication

You’ll already be aware that writing two variables directly next to each other means that they are multiplied, but what you might not have encountered before is the use of a dot $a \cdot b$ to denote multiplication. It does exactly the same job as the $\times$ sign; it’s just quicker to write. You do, of course, have to take care not to confuse it with a decimal point!

3.5, 3.6 Sum and product of a sequence

The Greek capital letter sigma, $\sum$ , means “the sum of” and is used for a set of discrete values. (The Latin letter summa, $\int$ , is the equivalent for continuous values; you’ll encounter this when you do integration, part of the field of Calculus.) The small numbers above and below the sigma tell you which terms of the sequence are being added, and the expression after the sigma defines the nth term of the sequence. For example:

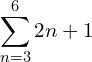$\displaystyle \sum_{n=3}^{6} 2n + 1$ or $\sum_{n=3}^{6} 2n + 1$

is the sum from the 3rd to the 6th term inclusive, of the sequence whose nth term is $2n + 1$ . If we write out the terms of the sequence we get

$2(3)+1, 2(4) + 1, 2(5) + 1, 2(6) + 1 = 7, 9, 11, 13$

so $\displaystyle \sum_{n=3}^{6} 2n + 1 = 7 + 9 + 11 + 13 = 40$ .

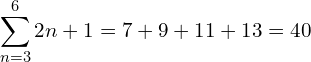Often you’ll see other letters, most usually $r$ or $i$ , used in place of $n$ .

The capital pi, $\prod$ , indicates the product of the successive terms, so you multiply rather than add them, but you’re less likely to encounter this one.

3.8 Modulus

The modulus, or magnitude, of a number is its absolute value, i.e. just its size, regardless of whether it’s positive or negative. Magnitude is also used to describe the length of a line or size of a vector, regardless of its direction.

For example, $|{-8}| = 8$ .

If a line goes from point A to point B then the length of the line can be expressed as $|AB|$ . If A is the point (2, 4) and B is (6, 7) then we can use Pythagoras to find its length:

$|AB|=\sqrt{(6-2)^{2}+(7-4)^{2}}=\sqrt{25} = 5$

3.9, 3.10 Factorials and combinations

$5!$ is pronounced “five factorial” and means $5 \times 4 \times 3 \times 2 \times1$ (or $5 \cdot 4 \cdot 3 \cdot 2 \cdot 1$ ), which of course gives 120.

Note: $0!$ is defined as 1 (otherwise you’re going to end up dividing by zero when it comes to working with $^nC_r$ ).

In Pure Maths you’ll learn how to expand brackets such as $(2 - 3x)^{7}$ without having to write the bracket out seven times and expand it all manually – this is called a binomial expansion. This also carries over into the Binomial Distribution topic in Statistics.

You’ll start by expanding the simpler $(1+x)^{n}$ and will find that the coefficients of the successive terms follow a pattern given by $^{n}C_{0}, ^{n}C_{1}, ^{n}C_{2}, ^{n}C_{3},$ etc., where $^{n}C_{r}$ is the number of possible combinations of r items chosen from a set of n. This could also be expressed as the number of ways of choosing r items from a set of n, so it’s sometimes pronounced “n choose r”.

So, for example, if you had the letters A, B, C and had to choose two of those then you could have A and B (the order doesn’t matter when you’re dealing with combinations, so AB is the same as BA), or B and C, or C and A, so that’s three possible combinations, i.e. $^{3}C_{2} = {{3!}\over{2!(3-2)!}}= 3$ .

The good news is that you don’t have to plug the factorials into the formula each time; there’s an $^nC_r$ function on your calculator.

Functions

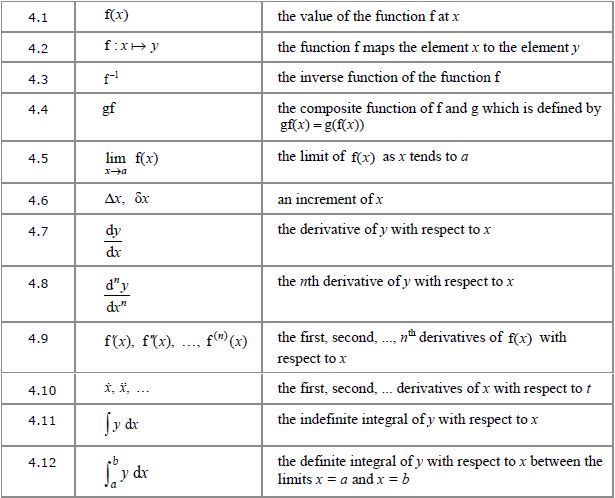
4.1 to 4.4 Basic function notation

You should already be familiar with this notation from GCSE, unless your exam board is OCR, in which case you might not have covered it yet. You’ll certainly be familar with the concept of function machines, where an input goes through a process to turn it into an output. The f here is simply a name for that process; g(x), h(x) etc, can be used to denote different functions.

So if $f(x) = 3x + 2$ then $f(4) = 3(4) + 2 = 14$ .

This definition of f can also be expressed as $f: x \mapsto 3x + 2$ , where the “ $\mapsto$ ” symbol means “maps to”.

4.5 Limit of a function

Sometimes a function will tend towards a particular limit; in other words, it will get closer and closer to a value but well never quite reach it. For example, consider the function

$f: x \mapsto 2^{x}$
or $f(x) = 2^{x}$

You should already know the shape of this graph; if you don’t, go to Desmos and put it in there.

When $x=0, f(x)=1$ .
For positive values of $x$ , $f(x)$ gets bigger and bigger.
But as we go to the left, looking at negative values of $x$ , the smaller $x$ gets, the closer $f(x)$ gets to zero… but it never quite gets there.

So the limit of $f$ as $x$ approaches $-\infty$ is zero, or $\displaystyle \lim_{x \rightarrow -\infty} f(x) = 0$ .

When a graph approaches a value but never quite gets there, we have an asymptote, so this particular graph has an asymptote at $y = 0$ or $f(x)=0$ .

4.6 to 4.12 Calculus notation

The remaining mathematical symbols in this section relate to the field of calculus, which is all about working with varying rates of change and finding areas under curves. If you’ve done the Edexcel International GCSE then you’ll have encountered differentiation already, but to most GCSE students this will be completely new.

Items 4.7/4.8, 4.9 and 4.10 in the table relate to differentiation; they are all different ways of denoting the rate of change of a function, which is the same thing as the gradient of the graph. (That’s the frist derivative; the second derivative is what you get when you differentiate twice, i.e. the rate of change of the gradient.) When you’re dealing with a straight line, of course, the gradient is constant, but when you have a curve it’s variable, so the gradient, as well as the curve itself, is a function of $x$ .

The last two items relate to integration, which is the opposite of differentiation. So if you have the gradient of the curve then you can integrate to find the equation of the original curve, or if you’re starting from the equation of the curve then integrating will give you the area under the curve. Essentially what you’re doing here is adding up the areas of an infinite number of very narrow strips, hence the use of the Latin summa ( $\int$ ) symbol to indicate a sum.

Exponentials and logarithms

Mathematical notation: Exponentials and logs

5.1, 5.2 The number “e”

You’re already familiar with the graphs of $y=2^{x}$ and $y=3^{x}$ . “ $e$ ” is an irrational number (roughly equal to 2.718) that has a special quality: the graph of $y=e^{x}$ has a gradient of $e^{x}$ . In other words the rate of change is exactly the same as the original function. You’ll use $e$ a lot in the later stages of the A-level course.

5.3, 5.4 Logarithms

A logarithm is another name for a power.

The log to base 2 of 8, $log_{2}8$ , is the power that you raise 2 to to get 8, i.e. 3.

So $log_{2}8=3$ is another way of writing $2^{3}=8$ .

Similarly, $log_{10}100=2$ because $10^{2}=100$

and $log_{3}{{1}\over{9}} =-2$ because $3^{-2}={{1}\over{3^{2}}}={{1}\over{9}}$

A logarithm with base $e$ is called a “natural logarithm”, written $ln$ , short for the Latin “logarithmus naturalis”. So $ln5$ is the same thing as $log_{e}5$ , or the power that $e$ needs to be raised to to get 5.

Trigonometry

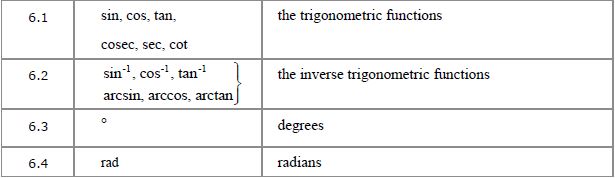
6.1, 6.2 The trigonometric functions and their inverses

You’re already familiar with sin, cos and tan (sine, cosine and tangent). Cosec, sec and cot are their reciprocals, i.e. ${\rm cosec} {x} = {{1} \over {\sin x}}$ , $\sec {x} = {{1} \over {\cos x}}$ , $\cot {x} = {{1}\over {\tan x}}$ .

You’ve encountered inverse trig functions before too. The table just shows two alternative ways of expressing them: $\arcsin x$ is the same thing as $sin^{-1} x$ .

6.4 Radians

Radians are an alternative unit for measuring angles. There are 2 $\pi$ radians in a circle so $\pi$ radians is the same angle as 180°.

Working in radians makes arc and sector problems simpler, but the main reason for using radians is that they’re essential for calculus involving trigonometry.

That’s all for this article. Here are links for the other parts:
Part 1: Set notation and miscellaneous symbols
Part 3: Vectors, Statistics and Mechanics

If you’ve found this article helpful then please share it with anyone else who you think would benefit (use the social sharing buttons if you like). If you have any suggestions for improvement or other topics that you’d like to see covered, then please comment below or drop me a line using my contact form.

On my sister site at at mathscourses.co.uk you can find – among other things – a great-value suite of courses covering the entire GCSE (and Edexcel IGCSE) Foundation content, and the “Flying Start to A-level Maths” course for those who want to get top grades at GCSE and hit the ground running at A-level – please take a look!

If you’d like to be kept up to date with my new content then please sign up to my mailing list using the form at the bottom of this page, which will also give you access to my collection of free downloads.

Please share this if you find it helpful!

2 Comments

Robert says:

29 December 2022 at 00:44

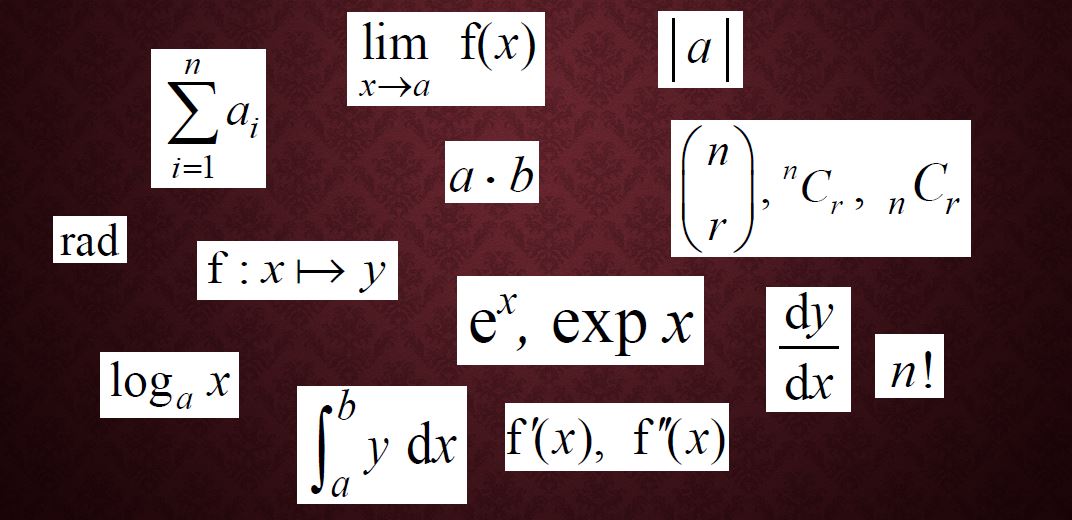
EDITOR’S NOTE:

Located on this page (see * address below), under the heading: ” 3.5, 3.6 Sum and product of a sequence”; the last clause of the last sentence reads: “… and the expression after the sigma DEFIES the nth term of the sequence.

Thanks for your attention.

*** https://b28mathstutor.co.uk/more-mathematical-notation-for-a-level/

1. Lynne Davis says:
  
  29 December 2022 at 10:45
  
  Thanks for pointing that out – now corrected.

More mathematical notation you need for A-level