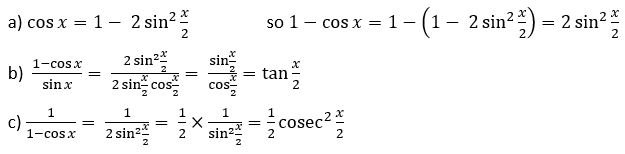Working with double angle formulae (A-level Maths)
The A-level Maths specification requires you to work with formulae for compound angles – sin (A ± B), cos (A ± B), tan (A ± B) – and use these to derive and use a range of double angle formulae, or double angle identities, which have a variety of applications. Sometimes half angles pop up too!
Compound angle formulae
For A-level Maths, you are given the following compound angle formulae (identities) in your formulae booklet:

You can use these, for example, to work out exact values for sin 15° or cos 75°, as well as in more complex problems; maybe I’ll write a more detailed post on that topic at some point.
But when you make A and B the same, so you’re adding two of the same angle, you get a new set of double angle formulae that have a whole new set of uses.
(You can, of course, ignore the versions of the formulae where the two angles are subtracted, since subtracting an angle from itself will leave you with zero!)
Deriving the double angle formulae
The sine formula
If we take the formula
sin (A + B) = sin A cos B + cos A sin B
and replace the B with another A,
then we get
sin (A + A) = sin A cos A + sin A cos A
which simplifies to the double angle identity
sin 2A = 2 sin A cos A
The tangent formula
Taking the formula
![]()
and replacing B with a second A, gives us
![]()
which simplifies to the double angle identity
![]()
The cosine formulae
The sine and tangent formulae have limited uses, but the cosine formula can be expressed in several different ways, making it much more versatile.
Taking the formula
cos (A + B) = cos A cos B – sin A sin B
and replacing B with a second A, gives us
cos (A + A) = cos A cos A – sin A sin A
which simplifies to the double angle identity
cos 2A = cos²A – sin²A
But since we know another identity connecting sin²A and cos²A, we can use that to eliminate either one of those terms:
sin²A + cos²A = 1
=> sin²A = 1 – cos²A
so the double angle identity becomes
cos 2A = cos²A – (1 – cos²A)
cos 2A = 2cos²A – 1
Similarly, cos²A = 1 – sin²A
which gives us
cos 2A = (1 – sin²A) – sin²A
cos 2A = 1 – 2sin²A
How can we use the double angle formulae?
1. Solving equations
Example 1
Solve 2sinθcos2θ – sin2θ = 0 for 0 ≤ θ ≤ 360°.
Have a go at the question yourself before looking at the solution. If you get stuck then peek at a line or two and see how much further you can get before you need to peek again!
Solution
The only thing we can replace sin2θ with is 2sinθcosθ, so let’s do that to start with:
2sinθcos2θ – 2sinθcosθ = 0
Now take 2sinθ out as a common factor:
2sinθ(cos2θ – cosθ) = 0
So either 2sinθ = 0
giving sinθ = 0 => the first three solutions are θ = 0, 180, 360°
… or cos2θ – cosθ = 0, which is going to take a little more work.
We can get the whole thing in terms of cos θ by using the double angle formula
cos 2θ = 2cos²θ – 1
so cos2θ – cosθ = 0 becomes
(2cos²θ – 1) – cosθ = 0, or
2cos²θ – cosθ – 1 = 0
This is a quadratic in terms of cosθ.
You might find it helpful to replace cosθ with u, so we have
2u² – u – 1 = 0
(2u + 1)(u – 1) = 0
So either 2u + 1 = 0, giving u = cosθ = -½
or u – 1 = 0, giving u = cosθ = 1
So the remaining solutions are
θ = cos¯¹(-½) = 120, 240°
θ = cos¯¹(1) = 0, 360° (a repeat of two of the earlier solutions).
2. Proofs
Example 2
Show that ![]() .
.
Again, see if you can work out the answer without peeking!
Solution
Replace sin 2θ with 2sinθcosθ.
We know that cot θ is ![]() or
or ![]() so that might be something to aim for. If we want the sin θ on the top of the fraction to cancel out then we need another sin θ on the bottom, so let’s replace cos 2θ with 1 – 2 sin²θ and see if that gets us anywhere.
so that might be something to aim for. If we want the sin θ on the top of the fraction to cancel out then we need another sin θ on the bottom, so let’s replace cos 2θ with 1 – 2 sin²θ and see if that gets us anywhere.
![]()
![]()
Now we can cancel top and bottom to give
![]()
(If you’d chosen a different formula for cos 2θ then you’d still have got there, but you’d have had to use another identity to simplify the denominator before cancelling. Try it and see!)
3. Calculus (differentiating and integrating)
By the time you get to the topics of compound and double angles, you’ll probably already have covered differentiation of sin x and cos x, including using the chain rule to differentiate sin 2x, cos 3x, etc… and the corresponding reverse processes for integration.
But you don’t yet know how to differentiate or integrate sin²x or cos²x. The double angle formulae for cos 2x allow us to get round this.
If we rearrange cos 2A = 2cos²A – 1 to make cos²A the subject then we get
cos²A = ½(cos 2A + 1)
Hence
∫cos²x dx
can be rewritten as
½∫ cos 2x + 1 dx
which of course integrates to ½ ( ½sin 2x + x) + c
or ¼ sin 2x + ½ x + c
Now your turn: Use a similar approach, starting with the identity cos 2A = 1 – 2sin²A, to find an expression for ∫sin²x dx.
You should end up with ½ x – ¼ sin 2x + c.
Half angle formulae
If we replace 2A with θ then we can rewrite the double angle formulae as follows:
sin 2A = 2 sin A cos A
becomes
sin θ = 2 sin ![]() cos
cos ![]()
cos 2A = cos²A – sin²A
becomes
cos θ = cos² ![]() – sin²
– sin² ![]() or
or
cos θ = 2cos² ![]() – 1 or
– 1 or
cos θ = 1 – 2sin² ![]()
And of course there’s the equivalent for tan 2A:![]()
becomes![]()
Now see if you can use these half angle formulae to answer the questions below:
I hope this article has helped you to understand how to obtain the double angle formulae – you need to be able to derive them yourself in the exam, unless you have them memorised – and how they can be useful.
I also have a series of three blog posts showing you all the mathematical notation you need for A-level, which you may find helpful:
Part 1: Set notation & miscellaneous
Part 2: Other Pure Maths notation
Part 3: Vectors, Statistics and Mechanics
If you’ve found this article helpful then please share it with anyone else who you think would benefit (use the social sharing buttons if you like). If you have any suggestions for improvement or other topics that you’d like to see covered, then please comment below or drop me a line using my contact form.
On my sister site at at mathscourses.co.uk you can find – among other things – a great-value suite of courses covering the entire GCSE (and Edexcel IGCSE) Foundation content, and the “Flying Start to A-level Maths” course for those who want to get top grades at GCSE and hit the ground running at A-level – please take a look!
If you’d like to be kept up to date with my new content then please sign up to my mailing list using the form at the bottom of this page, which will also give you access to my collection of free downloads.
Answers: