Forces and Newton’s Laws for A-level Maths

You’ve probably done some work on forces and Newton’s laws of motion in GCSE Physics or Combined Science, and that forms the basis of a lot of the work covered in the Mechanics element of A-level Maths. This article is intended mainly to reinforce the work you did at GCSE to make sure that you have a firm foundation for the more advanced topics.

In a future blog post I’ll be covering forces in equilibrium and resultant forces, and that leads on to problems involving connected particles, such as a car pulling a trailer or two bodies at opposite ends of a pulley. The image below shows a slightly more unusual scenario!

What is a force?

A force is a push or a pull that changes a body’s speed, direction of motion, or shape.
In A-level Maths we use only simplified models, so we don’t concern ourselves with changes of shape – but you do need to be aware of the effects of the simplifying assumptions.

When two objects interact, each of them exerts a force on the other.

Forces are measured in newtons (N), where 1 newton is 1 kg m s‾². (At A-level we usually write units using negative powers – e.g. ms‾² rather than m/s².) So 1 N is the force needed to make a mass of 1 kg accelerate at a rate of 1 m s‾².

Types of forces

You should be familiar with these types of forces:
friction, weight, tension, thrust, upthrust, air restistance, normal reaction.

Can you match the forces to their descriptions?

1. The force exerted by a body as a result of its mass combined with acceleration due to gravity.
   Always acts vertically downwards.
2. The reaction of a surface to the weight of a body placed on it; stops the body from falling
   straight through! Always acts perpendicular to the surface.
3. A force that resists motion. Caused by roughness where two surfaces are in contact.
4. Air’s version of friction; resists motion and so prevents a falling object from continuing to
   accelerate forever.
5. A pulling force in a taut string, wire or rod. Prevents two objects from moving further apart.
6. A pushing force in a rigid connector (a rod, not a string); prevents two objects from moving
   closer together.
7. A liquid’s version of friction, which acts on a body falling through it.

Click here for the answers

Newton’s laws of motion

These cover the basis of the study of statics (forces acting between stationary bodies) and dynamics (the relationship between forces and motion).

Newton’s first law

A body will remain at rest or continue to move with uniform motion in a straight line unless an external force acts on it.

In other words, forces do not cause motion in itself; they cause changes in motion, in the form of acceleration (positive or negative). If a body is moving with constant velocity and no forces are acting on it then it will continue to move at that velocity indefinitely.

Why doesn’t this happen in reality – for example if you nudge a coin across a smooth table, why doesn’t it just keep going?

Answer: Because there are always forces resisting motion and therefore causing deceleration, or negative acceleration. Typically these are air resistance and friction between surfaces; in reality no surface is completely smooth and so whenever there are two surfaces in contact there will be an element of friction.

Newton’s second law

This is sometimes given in a rather wordy form but basically boils down to the formula F = ma, where F is the resultant force in newtons, m is the mass in kilograms and a is the rate of acceleration in ms‾².

The acceleration is the change in motion caused by the resultant force. More on this later.

Newton’s third law

For every action there is an equal and opposite reaction.

Think of an object (e.g. a pen or book) sitting on a table. What forces are acting?
The object’s weight acts downwards, but there must also be a force of the same magnitude acting upwards to balance it, otherwise the object would fall straight through the table. This force is called the normal reaction, usually represented on diagrams by either N or R, and always acts in a direction normal – i.e. perpendicular – to the surface.

If the forces are balanced then the system is said to be in equilibrium and there will be no acceleration (but note that that doesn’t necessarily mean no motion – see first law!).

If the forces are not balanced then there is a resultant force and this will result in acceleration; this is where F = ma comes in.

For example, to produce acceleration of 5 ms‾² in a body of mass 3 kg, the resultant force required would be F = ma = 3 × 5 = 15 N.

Acceleration due to gravity

What we normally refer to as “gravity” is actually the acceleration due to gravity. Your weight is the pull that the Earth exerts on you. When we’re looking at the weight of a body, F = ma becomes W = mg, where W is the body’s weight in newtons (we don’t measure weight in kilograms – that’s mass!) and g is the acceleration due to gravity. On Earth, g is usually between 9.8 and 9.82 ms‾² depending on where you are.

(Scientists tend to be pragmatic and use 9.81, while mathematicians usually use 9.8 because that’s the correct rounded value for every possible value of g, although it does have the disadvantage of implying that g could be anywhere from 9.75 to 9.85!)

So if you have a mass of 70 kg (that’s about 11 stone) then your weight – on Earth – will be 70 × 9.8 = 686 N, or 690 N to 2 s.f.

Questions on forces and Newton’s laws:

1. What happens to you if you step off a platform that was moving at constant speed onto a stationary surface (e.g. off a moving bus onto the pavement, or off the end of a travelator)? Why is this?
2. If you drive fast enough with a dog loose in the boot of your car, will the dog stay pinned to the inside of the tailgate? Why or why not?
3. a) What would the acceleration be if you pushed a 20kg body across a smooth surface with a force of 30N?
   b) What force would be needed to cause the same acceleration in a 15kg body?
4. a) If acceleration due to gravity is 9.8 ms‾², what is the weight of a 1200kg car?
   b) What would its weight be on the Moon, where g = 1.6 ms‾²?

Click here for the answers

Force diagrams

Put an object (pen, eraser) on a book or board lying flat on the table (a horizontal plane). What forces are acting? Sketch a diagram, treating the object as a particle (i.e. it has mass but is of negligible size).

Done it?

Now gradually tilt the book/board. Sketch a diagram of the forces that are acting now. Why doesn’t the object slide down the plane as soon as it starts to tilt? What are the actions and corresponding reactions here?

What happens if you tilt the plane further? Why? What are the actions and corresponding reactions now?

Click here for the answers

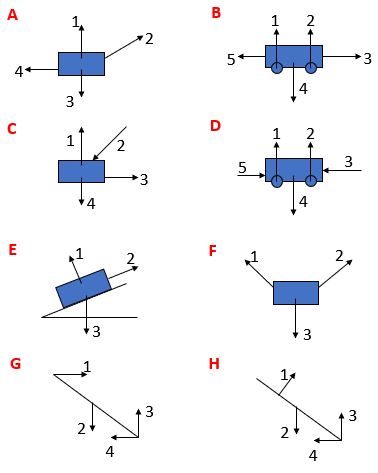
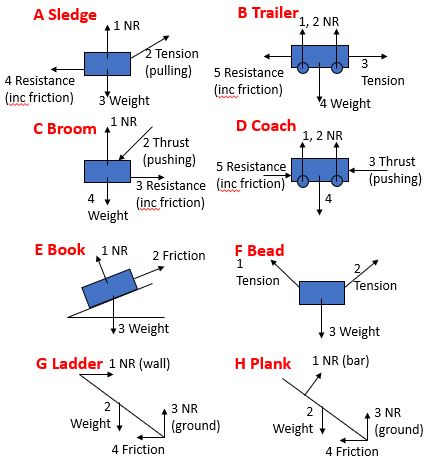
Force diagrams matching activity

Below are force diagrams showing the following:

• A trailer being towed by a car
• A coach being shunted (pushed) by a train engine
• A plank resting on a smooth bar with one end of the plank on rough ground
• A sledge being pulled along level ground
• A bead supported by a string threaded through it
• A ladder resting up against a smooth wall
• A broom head being pushed
• A book resting on a sloping desk lid.

Match the diagrams to the descriptions and label the forces 1, 2, 3, 4, 5 on each diagram using Tension, Thrust, Friction, Resistance, Weight, Normal reaction.

Click here for the answers

That’s it for the introduction to forces and Newton’s laws. I hope you’ve found it helpful.

This topic continues in this post on equilibrium and resultant forces.

---

Answers

Types of forces

1. Weight
2. Normal reaction
3. Friction
4. Air resistance
5. Tension
6. Thrust
7. Upthrust

Back to this section

Questions on forces and Newton’s laws

1. You will have to take a few quick steps to avoid falling over! Ignoring air resistance, there are no forces acting on you while you are moving at constant speed, but when you land on the stationary surface there is suddenly friction that prevents your feet from continuing to move in the same direction. The upper parts of your body, however, will keep moving in your previous direction of travel until a force is applied to slow them down. If you don’t move your feet to create that force then your body will rotate, using your “stuck” feet as a pivot, and you’ll fall over.
2. It will only stay pinned if you accelerate fast enough. If the car is travelling at constant speed then there are no resultant forces acting on bodies in the car (since F=ma, if a=0 then F=0) – there will only be a force when the car is accelerating or braking.
   Of course, this is why we have seatbelts: in a crash, the car decelerates extremely quickly but the passengers only decelerate when they are in contact with something stopping them from moving forwards. If you weren’t wearing a seatbelt then you’d be thrown into the windscreen or the seat in front of you.
3. a) F = ma => a = F/m = 30 / 20 = 1.5 ms‾²
   b) F = ma = 15 x 1.5 = 22.5 N
4. a) F = ma becomes W = mg so W = 1200 x 9.8 = 11760 N (or 12000 N to 2sf)
   b) On the Moon it would be 1200 x 1.6 = 1920 N.

Back to this section

Force diagrams

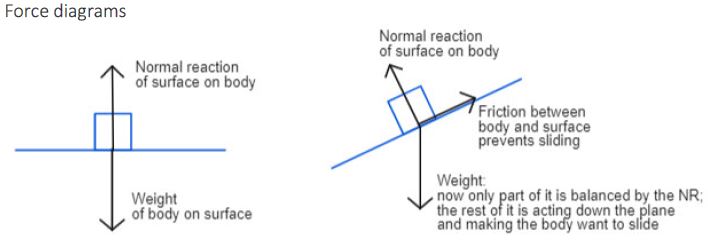
In the above diagrams the forces are in equilibrium, so there is no acceleration.
As the plane gets steeper, the component of the weight acting down the plane increases, until it overcomes the frictional force, so there is a resultant force acting down the slope and the body starts to slide – accelerates – in that direction.

Back to this section

Force diagrams matching

Back to this section