Graph transformations for GCSE and A-level Maths (Part 1)
In my tutoring, the topic of graph transformations is one that almost every Higher GCSE, IGCSE or A-level student wants to spend time on, so I thought I’d use it as the subject of a series of blog posts / tutorials. You can find Part 2 here, and Part 3 (for A-level only) here.
The only graph transformations included in the GCSE specification are translations and reflections, but the IGCSE and A-level specs also include stretches, and I’m really not sure why they missed them off the GCSE spec! All three are covered in this article.
Up to AS level you only need to be able to deal with a single graph transformation at a time (though that could include a translation with components going in both the x- and y-directions), but in the second year of A-level you also have compound transformations to deal with. I’ll cover those in a later article.
Graph transformation basics
General rules to remember
If the transformation involves adding or subtracting then the graph transformation is a translation. This means that the graph moves to a new position but doesn’t change shape.
translations are normally described with the word “translation” and a column vector such as ![]() .
.
(If you don’t understand column vector notation then take a look at my tutorial on understanding vectors here.)
If it involves multiplying or dividing then it’s a stretch, so the graph gets taller/shorter or wider/narrower.
When describing this type of graph transformation you must use the word “stretch”, say which direction it’s in and give the scale factor. Never refer to it as an enlargement, a squash or a shrink!
If a change of sign is involved then it’s a reflection. If it’s a vertical transformation then the mirror line is the (horizontal) x-axis, and if it’s a horizontal reflection then it’s in the (vertical) y-axis.
(Remember that the x-axis is also the line y = 0, and the y-axis is also the line x = 0!)
Of course, to change sign we multiply by -1, so a reflection could also be viewed as a stretch with scale factor -1… but you should treat stretches and reflections as separate transformations.
Vertical or horizontal?
If something has been done to the whole function then the transformation is vertical, or in the y-direction, and goes just as you’d expect.
If it’s only the “x” bit that’s been replaced by something else then the transformation is horizontal, or in the x-direction, and goes in the opposite direction to what you might expect. To decide how the transformation needs to be described, ask yourself how you would undo what’s been done to the x (I sometimes refer to this as “undressing” the x). This is a bit harder to get your head round, but a look at the examples a little further down should help.

Examples of vertical graph transformations:
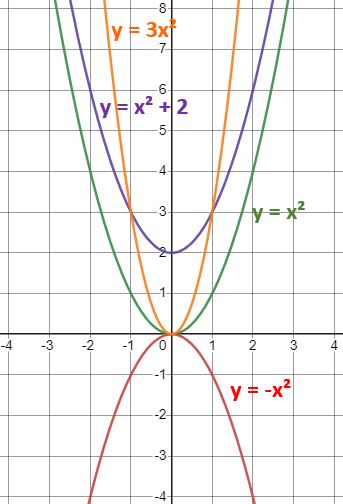
y = x²
→ y = x² + 2
(The arrow means “maps to”, or in this context “is transformed to”.)
2 has been added to each of the y-values so the whole graph moves up by two units; the transformation is a translation with vector ![]() .
.
y = x²
→ y = 3x²
All the y-values have been multiplied by 3; the transformation is a stretch in the y-direction with scale factor 3. You can also describe this as a “stretch parallel to the y-axis” but do NOT say it’s a “stretch in the y-axis”!
y = x²
→ y = -x²
All the y-values have been multiplied by -1, i.e. had their sign changed; the transformation is a reflection in the x-axis. In other words, it’s been flipped vertically, but you won’t get any marks for saying that in an exam!
The diagram below shows the original curve in green and each of the three graph transformations in a different colour: purple for the translated curve (moved up by 2 units), orange for the stretched one (three times the height, e.g. the point (1, 1) has moved to (1, 3)) and red for the reflected one.
Examples of horizontal graph transformations:
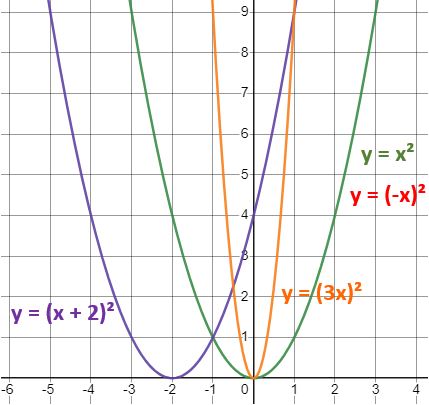
y = x²
→ y = (x + 2)²
The x has been replaced by x + 2; to get it back to being x on its own we need to subtract 2. Therefore the transformation is a translation with vector 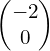 .
.
y = x²
→ y = (3x)²
The x has been replaced by 3x; to get it back to being its own we need to divide by 3. So the transformation is a stretch in the x-direction with scale factor ⅓. You can also describe this as a “stretch parallel to the x-axis” but do NOT say it’s a “stretch in the x-axis”!
Of course, (3x)² is the same as 9x², so this graph transformation could also be described as a stretch in the y-direction with scale factor 9.
y = x²
→ y = (-x)²
The x has had its sign changed; the transformation is a reflection in the y-axis. Of course the graph of y = x² is symmetrical about the y-axis so reflecting it in that line won’t change it at all!
The diagram below shows the original curve in green, the translated curve (2 units to the left) in purple, and the stretched one in orange. You can see that the orange curve is one third of the width, or nine times the height, of the original green curve; you could say that the point (1, 1) has been transformed to either (⅓, 1) or (1, 9), depending on which description you want to use.
The reflected curve isn’t shown (but is labelled in red) since it’s exactly the same as the original one.
Your turn
Now have a go at these questions to check your understanding of graph transformations. The answers can be found here.
A) Sketch the graph of ![]() , labelling any intercepts with the axes. (If you don’t know what it looks like then you can use Desmos – or other graphing software if you prefer – to help you.) What will the transformed graph look like and what will its equation be if it is:
, labelling any intercepts with the axes. (If you don’t know what it looks like then you can use Desmos – or other graphing software if you prefer – to help you.) What will the transformed graph look like and what will its equation be if it is:
- stretched in the y-direction with a scale factor of 3?
- stretched in the y-direction with a scale factor of ⅓?
- reflected in the x-axis?
- translated by vector
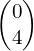 ?
? - translated by vector
 ?
? - reflected in the y-axis?
- stretched in the x-direction with a scale factor of 5?
- stretched in the x-direction with a scale factor of ⅕?
- translated by vector
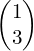 ?
?
B) Repeat (A) for the graph of ![]() .
.
C) Describe the following transformations. The ones marked with asterisks (*) have 2 possible answers, one horizontal and one vertical. Can you spot both?
- *
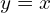 →
→ 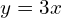
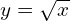 →
→ 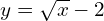
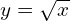 →
→ 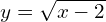
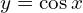 →
→ 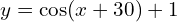
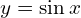 →
→ 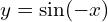
- *
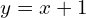 →
→ 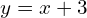
- *
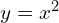 →
→ 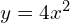
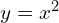 →
→ 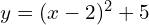
- *
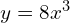 →
→ 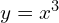 (Looking back at question 7 might help here.)
(Looking back at question 7 might help here.) - *
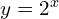 →
→ 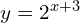 (Two different types of transformation here!)
(Two different types of transformation here!)
That covers the basics you need to know about graph transformations. (Remember, stretches aren’t included in the GCSE specification so you don’t need to worry about those if that’s the qualification you’re doing – though they’re good to know about anyway!)
In Part 2 we’ll do a bit more work on this topic and in Part 3 we’ll extend it to include compound transformations, as required for A-level.
If you’ve found this article helpful then please share it with anyone else who you think would benefit (use the social sharing buttons if you like). If you have any suggestions for improvement or other topics that you’d like to see covered, then please comment below or drop me a line using my contact form.
On my sister site at at mathscourses.co.uk you can find – among other things – a great-value suite of courses covering the entire GCSE (and Edexcel IGCSE) Foundation content, and the “Flying Start to A-level Maths” course for those who want to get top grades at GCSE and hit the ground running at A-level – please take a look!
If you’d like to be kept up to date with my new content then please sign up to my mailing list using the form at the bottom of this page, which will also give you access to my collection of free downloads.
Answers to graph transformations questions:
A)
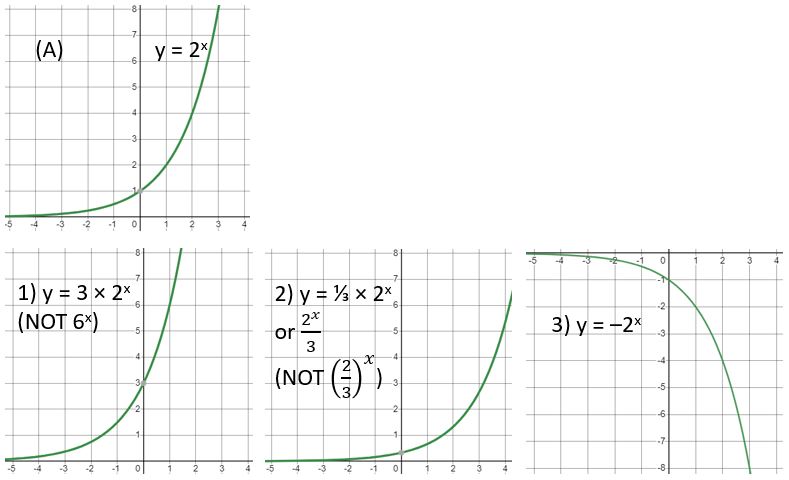
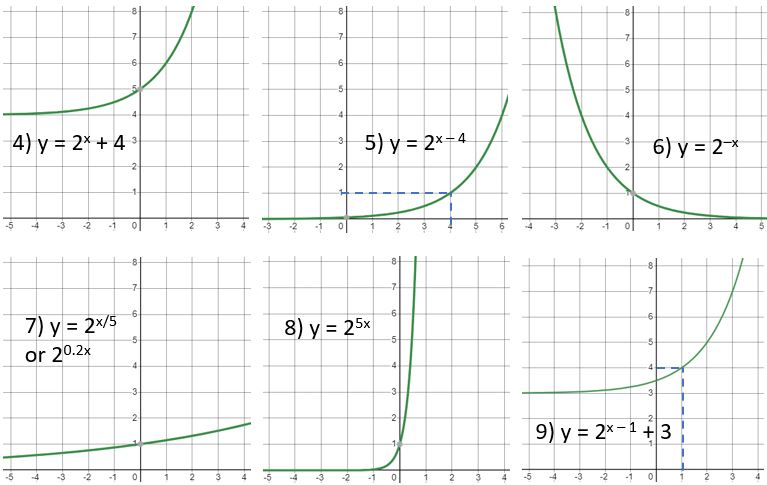
B)
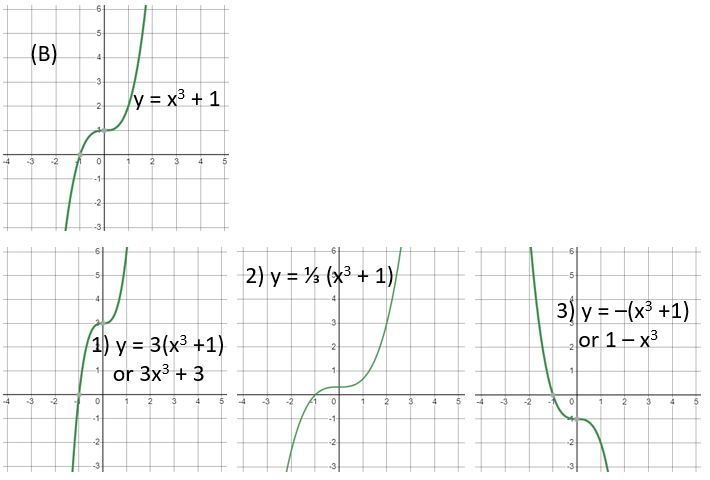
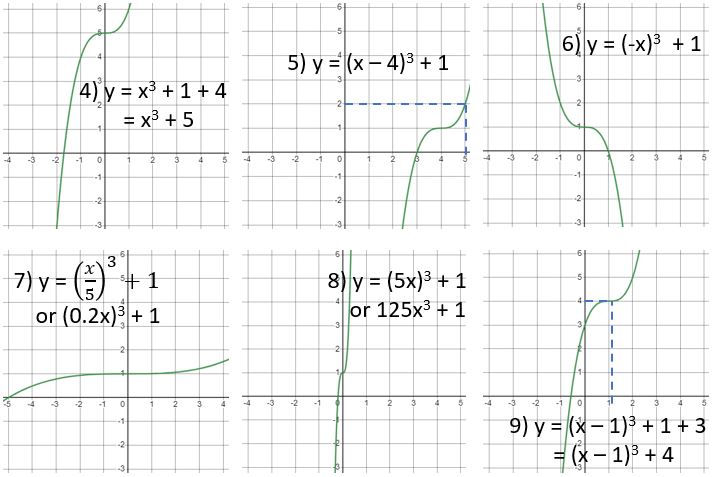
C)
- Stretch in the y-direction, SF 3 OR Stretch in the x-direction, SF ⅓
- Translation
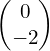
- Translation
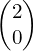
- Translation
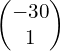
- Reflection in the y-axis (horizontal reflection)
- Translation
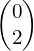 OR Translation
OR Translation 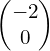
- Stretch in the y-direction, SF 4 OR Stretch in the x-direction, SF ½ (since 4x² can also be written as (2x)²)
- Translation
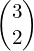 (You might recognise this as the completed square form of a quadratic – notice how the translation vector takes you from (0, 0) to the vertex of the translated curve.)
(You might recognise this as the completed square form of a quadratic – notice how the translation vector takes you from (0, 0) to the vertex of the translated curve.) - Stretch in the y-direction, SF ⅛ OR Stretch in the x-direction, SF 2 (since 8x³ can also be written as (2x)³)
- Translation
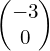 OR Stretch in the y-direction, SF 8. (To find the second one, apply the first law of indices – see tutorial here if needed – and then simplify.)
OR Stretch in the y-direction, SF 8. (To find the second one, apply the first law of indices – see tutorial here if needed – and then simplify.)

