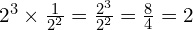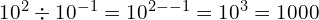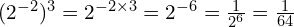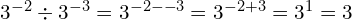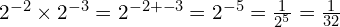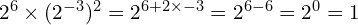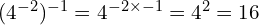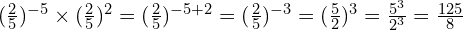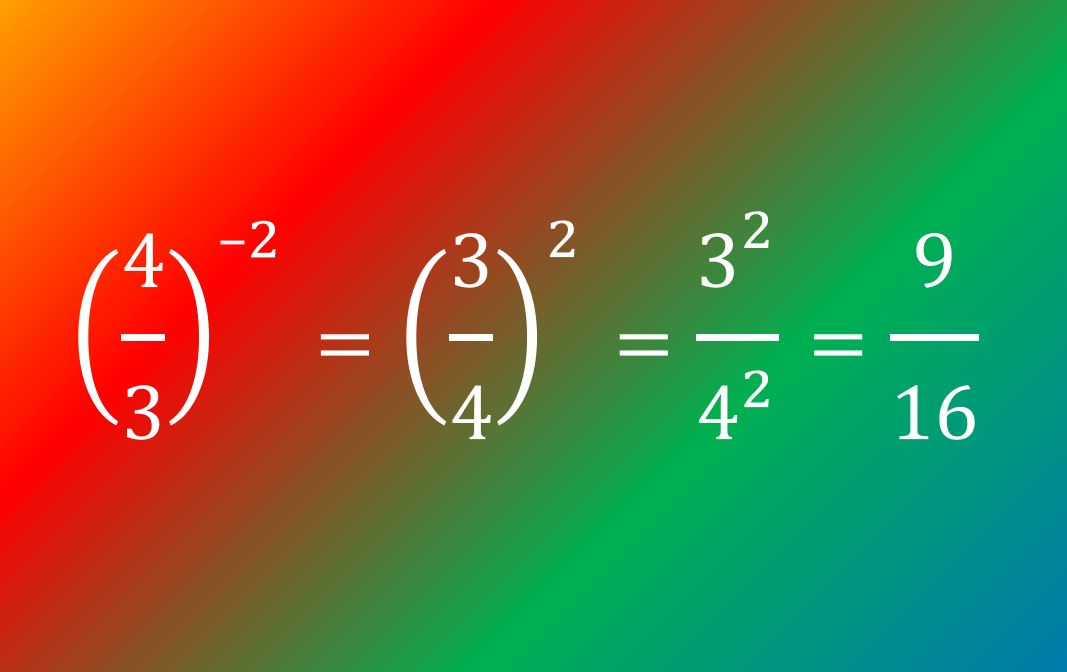Indices 1: Essential skills for GCSE and A-level Maths: Basics, index laws, negative indices
What are indices, and what do I need to know about them?
“Indices” is the plural of index. An index is another name for a power, also sometimes called an exponent. It’s a small number written as superscript, such as the ![]() in
in ![]() .
.
At Foundation GCSE you need to have an understanding of indices, and if you’re aiming for Grade 4 or above, that includes negative indices. You should understand what, for example, ![]() means, and be able to write numbers involving negative indices as ordinary fractions (which may be top-heavy). The image below gives an example – but don’t worry if it confuses you at first, just work through the lesson on this page and it will make a lot more sense by the time you get to the end!
means, and be able to write numbers involving negative indices as ordinary fractions (which may be top-heavy). The image below gives an example – but don’t worry if it confuses you at first, just work through the lesson on this page and it will make a lot more sense by the time you get to the end!
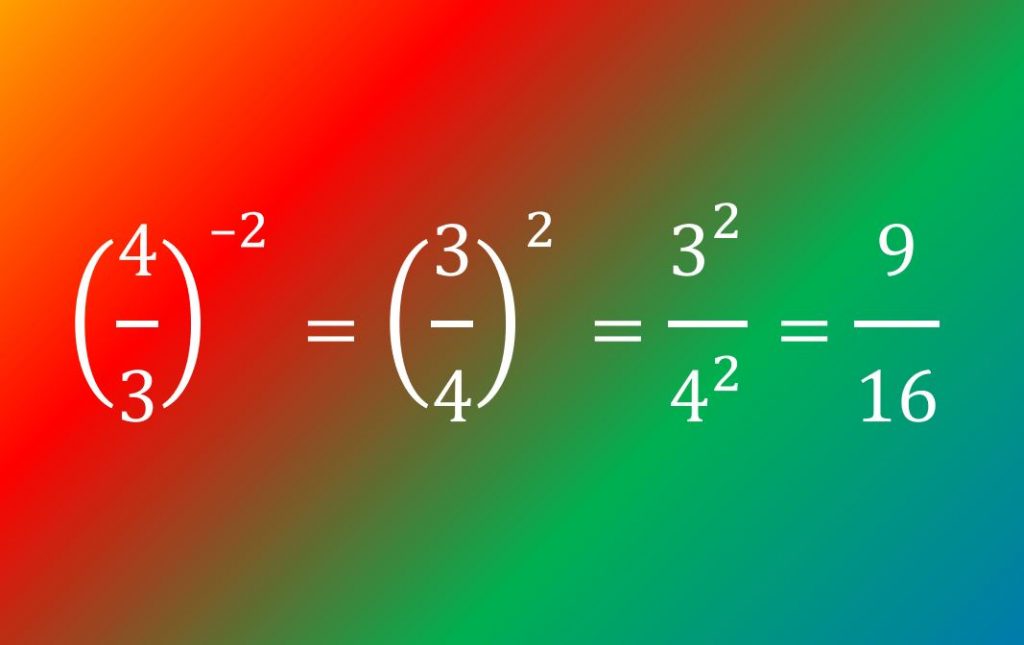
For Higher, the spec includes fractional indices, and you should be able to convert between index form and surd form.
In this article we’re going to cover the Foundation content, and in the next one we’ll look at the material you need for Higher GCSE.
If you’re going on to do A-level then it’s essential that you have a good grasp of the GCSE content on this topic, as you’ll be using it a lot. For more information on the GCSE skills that you need for A-level Maths, take a look at this blog post.
The basics: positive integer powers
A positive integer power tells you how many times a number is muliplied by itself:
![]()
![]()
![]()
![]()
(You can think of this last one either as ![]() or as
or as ![]() .)
.)
… and so on.
If you need to raise a fraction to a power then you raise both the numerator and the denomiator to that power, for example:
![]()
Your turn: Work out the values of:
Laws of indices
Write out each of these calculations in full and hence simplify them (you don’t need to work out the actual numerical values; just leave them in simplified index form, i.e. as ![]() ):
):
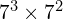
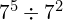 (Hint: write it as a fraction)
(Hint: write it as a fraction)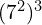
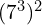
The answers you should have got are ![]() ;
; ![]() ;
; ![]() ;
; ![]() . Click here for a more detailed explanation.
. Click here for a more detailed explanation.
So what’s happened to the indices in each case? See if you can work out the general rules before you read any further.
Answers:
From (1), if you multiply the terms then you add the powers; from (2), if you divide the terms then you subtract the powers; and from (3) and (4), if it’s a power of a power then you multiply the powers.
These relationships lead us to the laws of indices:
- 1st law of indices:
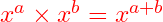
- 2nd law of indices:
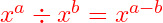
- 3rd law of indices:
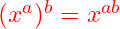
Note that the base – the number that’s being raised to the power – must be the same in each case. You can’t simplify, for example ![]() (other than by working out its numerical value), because the 2 and the 3 are different bases.
(other than by working out its numerical value), because the 2 and the 3 are different bases.
Now your turn: Simplify:
Now look again at question 4 above. How else could you write the simplified form of this, other than as a power of ![]() ? It might help you if you give
? It might help you if you give ![]() a value such as 2.
a value such as 2.
Hint: What do you get if you divide a number by itself?
Answer: ![]()
It doesn’t matter what the value of x is; anything to the power of zero is always 1.
Negative indices
Write out each of these calculations in full (using fractions) and hence put it into its simplest form.
Now apply the 2nd law of indices to each of the calculations above, and compare your answers in index form with the values you just worked out. Can you work out what a negative power means?
Answers:![]()
![]()
![]()
Generally, ![]()
So what would ![]() be?
be?
Answer: ![]()
(If that confuses you, think back to how you divide by a fraction: keep the first number as it is, flip the fraction that you’re dividing by, and multiply instead.)
So any number to the power of ![]() is its reciprocal.
is its reciprocal.
This meme might help you to remember how to deal with negative powers:

Now your turn: Evaluate:
Bringing it all together
Now see if you can combine the index laws with a mixture of positive and negative indices.
Evaluate:
Here’s a nice codebreaker activity to give you more practice with negative indices and laws of indices.
And that’s everything you need to know about indices for Foundation GCSE.
Part 2, on fractional indices, can be found here.
Answers
The basics
Laws of indices
![]()
![]() (cancel by dividing top & bottom by 7, twice)
(cancel by dividing top & bottom by 7, twice) ![]()
![]()
![]()
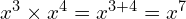
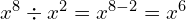
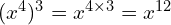
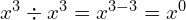
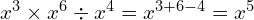 (do the calculation in any order, as long as you add the 3 and the 6 and subtract the 4)
(do the calculation in any order, as long as you add the 3 and the 6 and subtract the 4)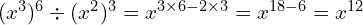
Negative indices
![]() (divide top & bottom by 2, three times)
(divide top & bottom by 2, three times) ![]()
![]()
![]()
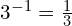
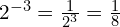
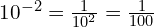 or
or 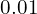
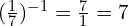
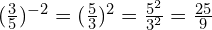
Bringing it all together
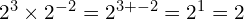 or
or