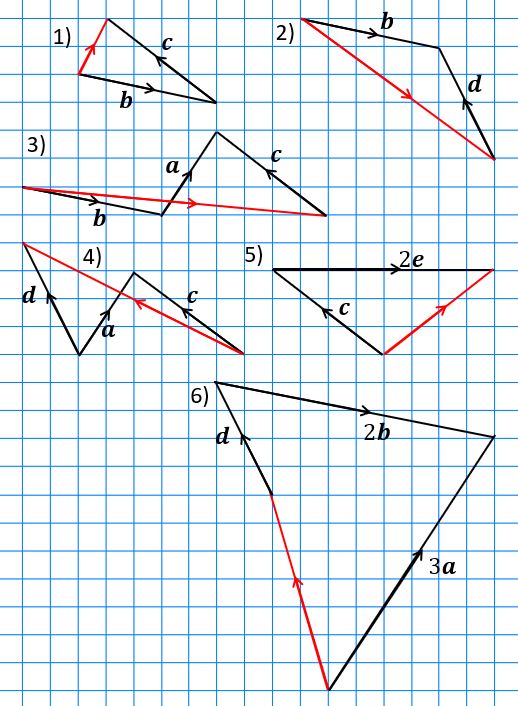
Understanding Vectors for GCSE Maths (Foundation Tier)
Vectors for GCSE Maths is one of the topics that people tend to find hardest. Some questions are very challenging even for the strongest students, but getting to grips with the basics isn’t so difficult. In this article we’re going to cover the Foundation content, and the next post will cover the Higher material.
Vectors for GCSE Maths – basics
A scalar quantity is just a number; it only has magnitude (size, e.g. length of a line).
A vector quantity has both magnitude and direction. It is usually represented on a diagram by a straight line with an arrowhead to indicate direction.

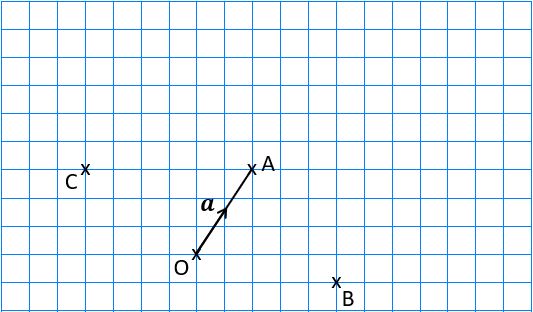
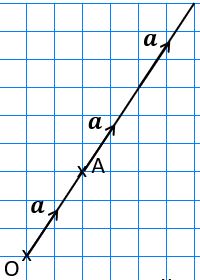
The journey from O to A on the diagram can be described by the vector ![]() .
.
We can also give the vector a lowercase name; let’s call it a. This uses bold type to indicate that it’s a vector; if you hand-write it then you should underline it.
Since it’s on a grid it can be written as a column vector: ![]()
– which means 2 to the right and 3 up.
The top figure is always how far to the right you are moving, and the bottom one is how far up – so if you’re moving to the left or down then the relevant value will be negative.
![]() only describes the movement from point O to point A, but a or the column vector form can be used anywhere.
only describes the movement from point O to point A, but a or the column vector form can be used anywhere.
How could you describe the movement from A to O as a vector?
Answer: ![]() or –a or
or –a or  (2 left and 3 down).
(2 left and 3 down).
Your turn
- Print out this PDF or copy the image above onto squared paper.
- Draw in the vector
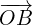 and label it b. (Don’t forget to underline your b since it’s handwritten!).
and label it b. (Don’t forget to underline your b since it’s handwritten!). - Draw in
 and label it c.
and label it c. - Express b and c as column vectors.
- Starting from C, draw in the vector
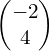 and label it d. Label its end-point D.
and label it d. Label its end-point D. - Starting from B, draw in the vector
 and label it e. Label its end-point E.
and label it e. Label its end-point E.
Check your answers here.
Scalar multiples
A vector can be multiplied by a scalar. For example, if you were to go from O to A and then carry on for twice as far again, then you’d have moved by vector ![]() .
.
The 3 is called a scalar multiple, and ![]() could also be described as 3a or
could also be described as 3a or 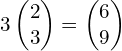
If one vector is a scalar multiple of another then the two vectors are parallel.
Your turn
- What would -2a look like? Show your answer as a diagram and as a column vector.
- Express
 c diagrammatically and as a column vector
c diagrammatically and as a column vector - Give a column vector parallel to b.
Check your answers here.
Adding and subtracting vectors
Adding vectors
Vectors can be added by placing them end-to-end.
So to find a+b we take a copy of b and add it to the end of a. Let’s call the point that it takes us to, P. The red arrow shows the resultant vector – i.e. the direct route from the start point to the end point of the combined vectors.
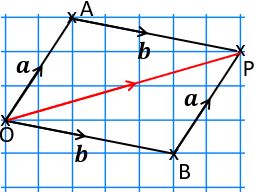
(Of course, b+a, with a added to the end of b, would give the same result – note the parallelogram shape.)
Adding the two column vectors gives 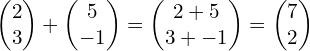
and you can see that this matches the vector ![]() , shown in red on the grid.
, shown in red on the grid.
(If you’re working in all one colour then you can use a double arrowhead ↠ to denote a resultant vector.)

So you can work out the sum of two column vectors without actually having to draw the diagram.
What about subtracting vectors?
To find a – b we need to put b on the end of a, but back to front… so you’re going forwards along a and then backwards along b. Again, the red arrow shows the resultant vector.

This time we have 
and you can see that this matches the resultant vector on the grid (3 to the left and 4 up).
Again, you don’t actually need to draw the diagram to subtract one column vector from another.
Going back to parallelogram OAPB, above, how could you describe ![]() in terms of a and b?
in terms of a and b?
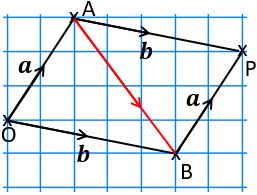
To get from A to B, you need to go backwards along a to O, and then forwards along b,
so that’s –a + b, which is the same thing as b – a.
Alternatively you could go forwards along b to P and then backwards along a, which gives the same result.
And in column vectors that’s
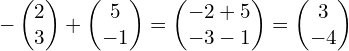
or
Of course b – a is the same as a – b but in the opposite direction – instead of 3 left and 4 up, we’re now going 3 right and 4 down.
When adding and subtracting vectors you’re not restricted to just two; you can add and subtract as many as you like, simply by putting them end-to-end in the correct orientation.
Your turn
Here’s a reminder of the column vectors from the first set of questions:
a = ![]() , b =
, b = 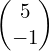 , c =
, c = 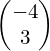 , d =
, d = 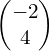 , e =
, e = ![]()
Find the resultant of each of the following combinations of these vectors, also drawing each combination on squared paper:
- b + c
- b – d
- b + a – d
- c – a + d
- c + 2e
- 3a – 2b – d
Check your answers here.
That covers the Foundation content on Vectors for GCSE Maths. You can find the post on the Higher content here.
If you’ve found this article helpful then please share it with anyone else who you think would benefit (use the social sharing buttons if you like). If you have any suggestions for improvement or other topics that you’d like to see covered, then please comment below or drop me a line using my contact form.
On my sister site at at mathscourses.co.uk you can find – among other things – a great-value suite of courses covering the entire GCSE (and Edexcel IGCSE) Foundation content, and the “Flying Start to A-level Maths” course for those who want to get top grades at GCSE and hit the ground running at A-level – please take a look!
If you’d like to be kept up to date with my new content then please sign up to my mailing list using the form at the bottom of this page, which will also give you access to my collection of free downloads.
Answers
Vector basics

Scalar multiples
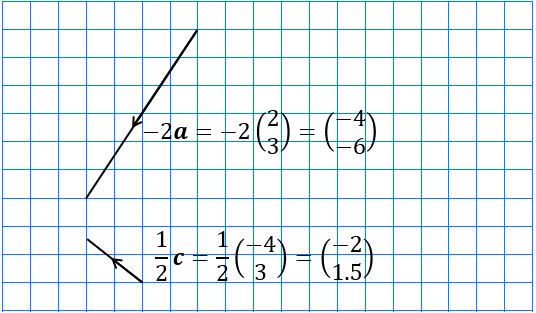
Examples of vectors parallel to b are 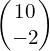 and
and  .
.
Adding and subtracting vectors