More graph transformations
This is Part 2 of a three-part tutorial on graph transformations; Part 1 can be found here. If you haven’t already worked through Part 1 then I recommend you look at it before trying to make sense of this one!
Part 3 covers compound graph transformations, which you don’t need to deal with until the second year of the A-level course, and can be found here.
A quick recap
Basic rules for graph transformations
The table below summarises the rules you need to remember.

Remember, the GCSE spec doesn’t include stretches, though Edexcel IGCSE and A-level both do.
Skills covered so far
In Part 1 we practised the following skills:
- Given an original graph and the description of a transformation, finding the equation of a transformed graph and sketching it
- Given the equations of an original and a transformed graph, identifying the transformation that has taken place
In Part 2 we’re going to do some more graph sketching – but this time for a graph whose equation we don’t know! – and in Part 3 we’ll then move on to the A-level skills of working with compound graph transformations.
Graph transformations where the equation is unknown
The JCQ regulations allow the use of graphical calculators in exams (yes, even in GCSE exams, though not many people use them at that level) but graphical calculators are expensive!
So that the owners of graphical calculators don’t have an unfair advantage over those who just have scientific ones, examiners like to write their questions in such a way that you have to demonstrate your understanding of a concept rather than just getting the answer from the calculator. Here’s an example of how they might do this…
Below is the graph of y = f(x).
As you can see, four coordinate points are marked on the graph. Your task is to
(a) sketch each of the transformed graphs listed under “Your turn” below, giving the coordinates of the new position of each of the four marked points, and
(b) describe the transformation in each case.
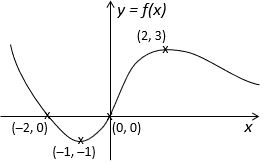
Bear in mind that
- A transformation in the x-direction will change only the x-coordinates, and
- A transformation in the y-direction will change only the y-coordinates.
Your turn
Now try sketching:
- y = 2f(x)
- y = f(2x)
- y = f(x) + 1
- y = f(x + 1)
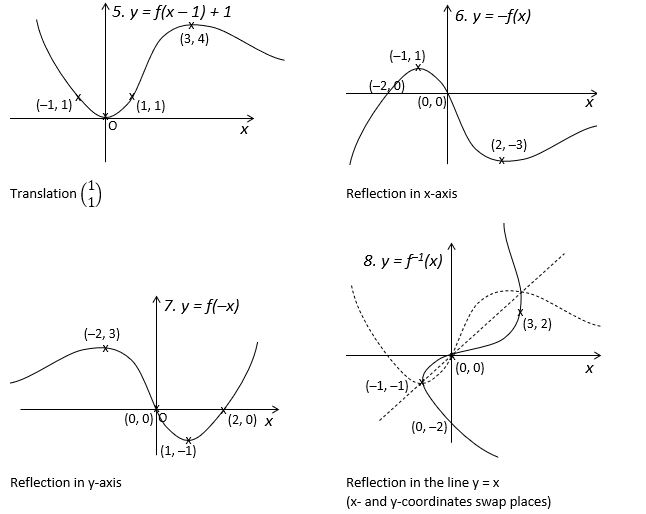
- y = f(x – 1) + 1
- y = -f(x)
- y = f(-x)
- y = f‾¹(x) (not strictly in this topic but you should know it if you’ve covered Functions)
Refer back to the summary table if you need to, and scroll down for some hints if you’re struggling!
Hints:
- y = 2f(x): multiplying the whole thing
- y = f(2x): multiplying only the x part
- y = f(x) + 1: adding to the whole thing
- y = f(x + 1): adding to only the x part
- y = f(x – 1) + 1: both directions, but positive or negative?
- y = -f(x): changing sign of the whole thing
- y = f(-x): changing sign of only the x part
- y = f‾¹(x) : the inverse function – reflect in what line? What does that do to the coordinates?
Click here for the answers and a summary of the effect of each transformation
That’s it for single graph transformations, and covers everything you need up to the end of AS-level Maths for this topic. In Part 3 we’ll look at compound transformations, as required for the second year of A-level Maths.
If you’ve found this article helpful then please share it with anyone else who you think would benefit (use the social sharing buttons if you like). If you have any suggestions for improvement or other topics that you’d like to see covered, then please comment below or drop me a line using my contact form.
On my sister site at at mathscourses.co.uk you can find – among other things – a great-value suite of courses covering the entire GCSE (and Edexcel IGCSE) Foundation content, and the “Flying Start to A-level Maths” course for those who want to get top grades at GCSE and hit the ground running at A-level – please take a look!
If you’d like to be kept up to date with my new content then please sign up to my mailing list using the form at the bottom of this page, which will also give you access to my collection of free downloads.
Answers:
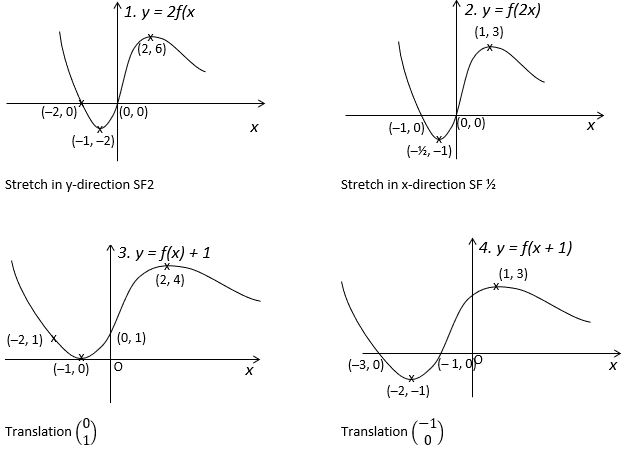
- y = 2f(x): the value of every y-coordinate is doubled
- y = f(2x): the value of every x-coordinate is halved
- y = f(x) + 1: every y-coordinate is increased by 1
- y = f(x + 1): every x-coordinate is decreased by 1
- y = f(x – 1) + 1: x-coordinates + 1, y-coordinates + 1
- y = -f(x): every y-coordinate changes sign
- y = f(-x): every x-coordinate changes sign
- y = f‾¹(x) : reflect in the line y = x; the x- and y-coordinates in each coordinate pair swap places

