Using Ratio mode on your Classwiz calculator

All the Casio Classwiz calculator models – both the original “X” and the new “CW” models – feature ratio mode, which didn’t exist on their predecessor the fx-83/85 GT Plus. Although it’s perfectly possible to get by without ever using ratio mode, it can be very handy in a wide variety of situations involving proportional reasoning.

Here are some examples – taken from my new calculator skills course – showing you how versatile ratio mode can be.

What is ratio mode useful for?

Ratio mode can be used:

• To find an unknown value in an equivalent ratio, for example:
  • an unknown share of an amount split in a given ratio
  • the cost of a different amount of something
  • a missing side when working with similar shapes
  • measurements with scale models and map scales
  • a different percentage of an amount from the one you’ve been given
  • journey time for a different distance at the same speed
• To find an unknown numerator or denominator in an equivalent fraction
• To help with calculations involving direct proportion

How to get into ratio mode

To enter ratio mode, you need to start by going to the main menu. To do that on the fx-83/85 GT X or the fx-991EX, you press the MENU button (top right); on the fx-83/85 GT CW or the fx-991CW, you press the HOME button (top left).

Then you use the arrow keys to highlight ratio mode – the one with two squares, as shown in the image below – and press [=], EXE or OK, depending what calculator you’ve got. (On the X models you also have the option to use keyboard shortcuts, but, in their wisdom, Casio have done away with these on the CW models.)

Getting into Ratio mode. Left to right: fx-85GT X, fx-991EX, fx-83GT CW, fx-991CW

You then get two options: 1: A:B = X:D, and 2: A:B = C:X.
The X is the unknown value that the calculator will find for you.

Note: Where the instructions tell you to press [=], that’s the EXE button on the CW models.

A few examples

1. Basic ratio example

If the members of a club are divided M : F in the ratio 2 : 3 and there are 58 males, how many females are there?

Answer:

1. Select option 2: A:B = C:X.
2. A:B is the known ratio, so put in 2:3 (so the first number represents the male proportion) by pressing [2] [=] [3] [=].
3. For the unknown ratio, the known (male) value is 58, so type that in, and press [=]. The X will be the number of females.
4. Press [=] again, and the calculator tells you that X = 87.

In other words, the relevant equivalent ratio to 2 : 3 is 58 : 87, so if there are 58 males then there must be 87 females.

Now that you’ve seen the basics of how to use ratio mode, see if you can predict how to answer the questions in the other examples before looking at the answers.

2. Using equivalent fractions to find the total

If the members of a club are divided M : F in the ratio 2 : 3 and there are 58 males, how many members are are there in total?

Of course, you could just work out the number of females, as in example 1, and then add the number of males and number of females together, but here’s an alternative method…

Answer:

1. Select option 2: A:B = C:X.
2. This time we’re using the fact that the number of males is of the total – but to use ratio mode we need to write it as 2:5
3. For A:B, put in 2:5 (so the first number represents the male proportion) by pressing [2] [=] [5] [=].
4. For the unknown ratio, the known (male) value is 58, so type that in, and press [=]. The X this time will be the total membership.
5. Press [=] again, and the calculator tells you that X = 145.

What we’re really doing here is using ratio mode to find an equivalent fraction: is equivalent to .

Similarly, you could use it to find what would be if you expressed it as an equivalent fraction with a denominator of 323:
Select A:B = X:D
Put in 5 for A and 17 for B, and 323 for D, and you should get X = 95
so .

3. Cost of a different amount

If 15 coffees cost £41.25,
a) how much would it cost for 24 coffees?
b) how many coffees would £90 buy?

Answer to (a):

1. Select option 2: A:B = C:X.
2. For A:B, put in 15 : 41.25. For C, put in 24.
3. Press [=] again, and the calculator tells you that X = 66 – i.e. that 24 coffees will cost exactly £66.00.

Answer to (b):

1. Select option 2: A:B = X:D.
2. For A:B, put in 15 : 41.25. For D, put in 90.
3. Press [=] again, and the calculator tells you that X = 32.727 – i.e. that £90 will buy 32-and-a-bit coffees, but isn’t enough for 33 – so your answer is 32.

You can use this approach for recipes too.
For example if a recipe for 16 fairy cakes uses 200g of flour, how much flour will you need to make 40 cakes? How many cakes can you make with 350g of flour?

And here’s an example using travel:
Travelling at a certain speed, a journey of 30 miles takes 48 minutes. How long will a journey of 50 miles take at the same speed?

Try those two questions; you should get answers of 500g, 28 cakes and 80 minutes.

4. Similar shapes

Given that shapes P and Q are similar, find length x.

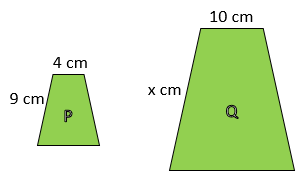
Answer:

There are several ways to do this.
We can either use the ratios of the sides within each shape, so 9 : 4 = x : 10  (or 4 : 9  = 10 : x)
… or we can use the ratios of corresponding sides on the two shapes: 4 : 10 = 9 : x (or 10 : 4 = x : 9).

Let’s do the first option:

1. Select option 1: A:B = X:D.
2. For A:B, put in 9 : 4. For D, put in 10.
3. Press [=] again, and the calculator tells you that X = 22.5.

Now try some of the other ways and check that you get the same answer.

5. Scale models and map scales

A model car is being built on a scale of 1 : 40. If the real car is 4.3 m long, how long will the model be, in centimetres?

Answer:

As we want the answer to be in cm, we can either work in cm all the way through, or work in metres and then convert to cm at the end.

Let’s use cm throughout:
Length of real car = 4.3 m, so that’s 430 cm.

In the ratio of 1 : 40, the 1 represents the model (the real car is 40 times the length), so we need
1 : 40 = x : 430

1. Select option 1: A:B = X:D.
2. For A:B, put in 1 : 40. For D, put in 430.
3. Press [=] again, and the calculator tells you that X = 10.75, so the model will be 10.75 cm long.

If we’d used 4.3m instead of 430 cm then we’d have got a model length of 0.1075 m, which we’d then have had to convert to 10.75 cm.

Map scales work in the same way, just with bigger numbers – for example the ratio might be 1 : 25000 – so the unit conversions can be trickier.

6. Finding a percentage

A jacket is sold with 15% off and costs £41.65 after the discount. What was its original price?

Answer:

The original price was 100%, so with 15% taken off, the price paid was 85% of that.

So we know that £41.65 is 85% of the original price, and we want to know what 100% of that price was.

1. Select option 2: A:B = C:X.
2. For A:B, put in 85 : 41.65. For C, put in 100. The X will be the original (100%) price.
3. Press [=] again, and the calculator tells you that X = 49, so the original price was £49.00.

Of course you can use this approach to find any percentage, not just 100%.

7. Direct proportion

y is directly proportional to x. When x is 3, y is 18.6. Find
a) y when x = 5
b) x when y = 68.2

Answer to (a):

1. Select option 2: A:B = C:X.
2. For A:B, put in 3 : 18.6. For C, put in 5.
3. Press [=] again, and the calculator tells you that X = 31 – i.e. that when x = 5, y = 31.

Answer to (b):

1. Select option 1: A:B = X:D.
2. For A:B, put in 3 : 18.6. For D, put in 68.2.
3. Press [=] again, and the calculator tells you that X = 11 – i.e. that when y = 68.2, x = 11.

With a little extra work, you can also use this where y is proportional to, for example, x². 
For example: y ∝ x² and when x = 2, y = 28. Find a) y when x = 5;  b) x when y = 252.

For a), use 2: A:B = C:X, but where you put the x-values, remember to put in x² instead, so you have 4 : 28 = 25 : X.

For b), use 1: A:B = X:D, again putting x² in for A. The “X” value that the calculator gives you will be x², so you need to square root it to get your x.

Conclusion

As you can see, ratio mode has lots of applications – if it’s a proportional reasoning question then you can probably use ratio mode to help you with it. As I said earlier, you can manage without it, but it’s nice to have!

To find out more about the clever stuff your calculator can do, take a look at my calculator skills course.

If you’d like to know more about the different calculator models then take a look at these two articles:

• The new Casio Classwiz CW calculators
• Clueless about calculators? Get more clarity here! – covers which calculators are suitable / admissible for which exams