How to resolve a vector into components
In the first year of A-level Maths, all the vectors you deal with are given to you in component form, i.e. as two perpendicular components, e.g.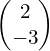 
or 2i – 3j. In the second year, however, you’re more likely to be given the magnitude and direction of the vector – often, but not always, a force – and have to work out the perpendicular components for yourself.
So here’s how to resolve a vector into components.
(Note: component form is sometimes referred to as rectangular form, and magnitude-direction form as polar form.)
Relevant past blog posts
If this article leaves you feeling a bit lost then you might find it helpful to first read some of the content of these blog posts on related topics:
Understanding vectors (Foundation GCSE)
Handling vectors for Higher GCSE
Forces and Newton’s Laws for A-level Maths (an introduction)
Equilibrium and resultant forces (A-level Year 1)
Resolving into components
Example:
A missile is fired at an initial velocity of 50ms-1 and at an angle of 35° with the horizontal. Find the horizontal and vertical components of its initial velocity.
Magnitude of vector = u = 50
Let’s call the horizontal component u
and the vertical component u
.
If you move the vertical arrow to the right of the diagram then you can see that u, u and u form a right-angled triangle where
cos 35° 
so u = 50 cos 35° = 41.0 ms¯¹ (3 s.f.)
sin 35° 
so u = 50 sin 35° = 28.7 ms¯¹ (3 s.f.)
So this vector can be written in component form as (41.0i + 28.7j) ms¯¹ or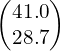 
ms¯¹.
The “cos-y” component
To remember which trig ratio to use where, you might find it helpful to identify the “cos-y” component: the one that has the given angle tucked in “cosy” between it and the original vector is the one to use cos with. In the above example that’s the horizontal component, but that’s not always the case.
For the other component, you can remind yourself to use sine by thinking “it’s a sin to go away from the angle”!
The diagram below shows how to apply this to the same example as before, but with different angles defined. Of course we still get the same value for each component, because cos 35° = sin 55° and vice versa.
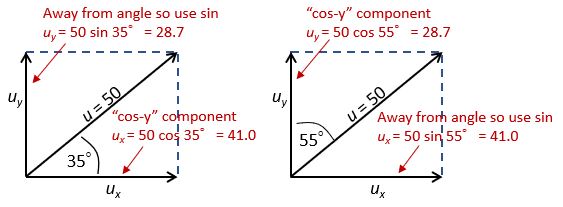
In general, a vector V of magnitude V and angle θ with the positive i-direction (as in the left-hand diagram above) can be written in component form as
V = V cos θ i + V sin θ j
Finding the angle / unknown component
If you know the magnitude and one component of a vector then you can deduce the other component and angle at which the vector is acting.
Example:
The vector v, of magnitude 30 units and acting at an angle of θ above the positive i-direction (i.e. the x-axis), has a horizontal component of 17 units. Find θ and the vertical component of the vector.
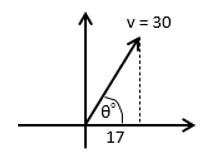
Solution:
The horizontal component is given by v cos θ, so
30 cos θ = 17
=> cos θ = 
=> θ = 55.5° (3 s.f.)
Now that we know the value of θ, we can of course find the vertical component, which in this case will be positive since we know that θ is above the x-axis:
Vertical component of v = 30 sin 55.5° = 24.7 units
(You could, of course, have found the vertical component using Pythagoras instead.)
Note: The Rec function on your calculator can also be used to convert a vector from polar (magnitude-direction) form to rectangular (perpendicular components) form, and the Pol function goes the other way. In each case, θ is the angle with the positive x-axis.
Resolving a force into components
We resolve forces into perpendicular components in exactly the same way as we do other vectors:
In this diagram, force F can be resolved into
horizontal component Fh = F cos θ and
vertical component Fv = F sin θ
Remember to check that your calculator is in the correct mode (degrees or radians)!
Working the other way, Fh2 + Fv 2 = F2
and tan θ = 
In some cases you’ll need to resolve parallel and perpendicular to a slope rather than horizontally and vertically, but it works in the same way; just treat the slope as the x-axis.
Your turn
Always use a diagram!
- Resolve these vectors and express in component form to 1 d.p. (Remember that some of the components will be negative!)
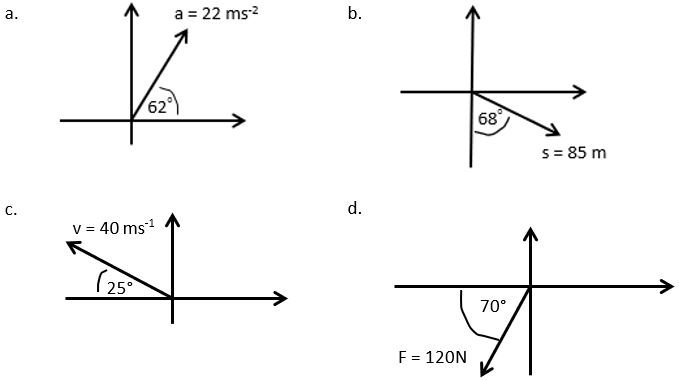
- For each of the forces below, sketch a diagram and find the horizontal and vertical components:
- 100N, 23° above positive horizontal
- 250N, 30° below positive horizontal
- 34N, acting upwards 20° to left of vertical
- For each vector, sketch a diagram and find the unknown angle, and hence express as a column vector:
- 65 m at θ° above the positive i-direction, magnitude of horizontal component = 50 m
- 15 ms-1 at θ° below the positive i-direction, magnitude of horizontal component = 4 ms-1
- 50 N at θ° below the negative i-direction, magnitude of vertical component = 42 N
If you’ve found this article helpful then please share it with anyone else who you think would benefit (use the social sharing buttons if you like). If you have any suggestions for improvement or other topics that you’d like to see covered, then please comment below or drop me a line using my contact form.
On my sister site at at mathscourses.co.uk you can find – among other things – a great-value suite of courses covering the entire GCSE (and Edexcel IGCSE) Foundation content, and the “Flying Start to A-level Maths” course for those who want to get top grades at GCSE and hit the ground running at A-level – please take a look!
If you’d like to be kept up to date with my new content then please sign up to my mailing list using the form at the bottom of this page, which will also give you access to my collection of free downloads.
Answers
1) a) (10.3i + 19.4j) ms-2 b) (78.8i – 31.8j) m c) (-36.3i + 16.9j ) ms-1 d) (-41.0i – 112.8j) N
2) 1) 
N 2) 
N 3) 
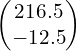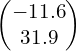N
3) 1) θ = 39.7°;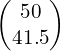 
m 2) θ = 74.5°; 
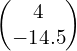ms¯¹ 3) θ = 57.1°; 
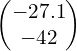N
