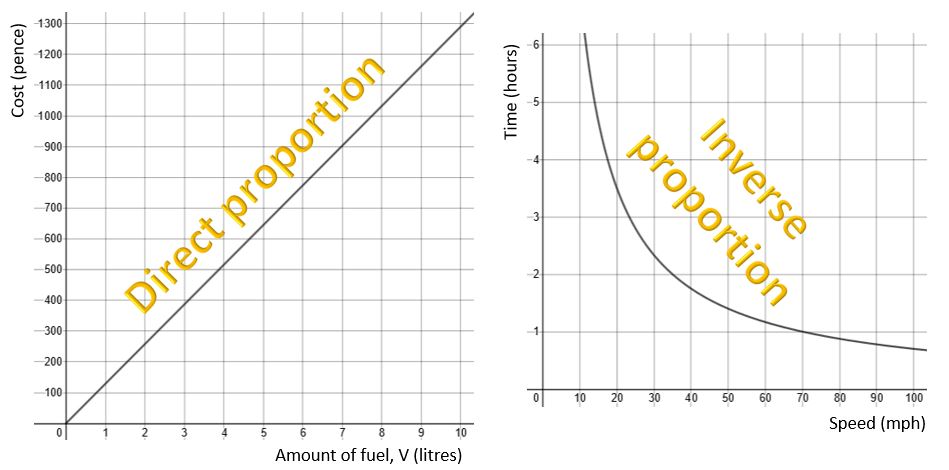
Direct and inverse proportion for Higher GCSE
For Foundation GCSE you just need to know what equations and graph shapes represent direct and inverse proportion, and work with equations given to you. That’s all covered in a previous article which you can find here.
For Higher you have to actually derive the equations, and work with some more complex relationships. Of course you need to know the Foundation content too, so it’s worth taking a look at the post linked above before you work through this one.
Direct proportion
Simple direct proportion
y is directly proportional to x (written in mathematical notation as ![]() ) if, when x doubles, y doubles. If x is multiplied by 10 then y is also multiplied by 10; if x is halved then so is y.
) if, when x doubles, y doubles. If x is multiplied by 10 then y is also multiplied by 10; if x is halved then so is y.
Sometimes you might also hear the expression “y varies as x“, which means the same thing.
This can be written as an equation (really it’s a formula, since there are two variables) like this:![]()
where k is a constant, called the constant of proportionality.
For example:
- Time T for a decorator to decorate n rooms is proportional to the number of rooms. If it takes k hours to decorate one room, then the time T taken to decorate more than one room will be the k hours multiplied by the number of rooms, giving T = kn
- The cost, C, of fuel is proportional to volume, V litres, purchased. If it costs k pence for 1 litre of fuel then V litres will cost V x k, giving a total cost (in pence) of C = kV
At Higher Tier you will normally be give a pair of values for the variables, and you are expected to convert the statement of proportionality into an equation and work out the value of k.
Example 1
The mass of a metal rod is directly proportional to its length. If a rod 0.6 m long has a mass of 3.3 kg, use an equation of proportionality to find
(a) the mass of a rod 2 m long;
(b) the length (to the nearest cm) of a rod with a mass of 8 kg.
Solution
If we use M for mass and L for length then ![]()
which gives us ![]()
We know that when L = 0.6, M = 3.3, so substitute in those values and work out what k must be:
![]()
![]()
![]()
So the equation is ![]()
Now we can use the equation to answer the questions:
(a) When L = 2, we have M = 5.5 × 2 = 11 kg
(b) When M = 8, we have 8 = 5.5 L
so L = 8 ÷ 5.5 = 1.454545… = 1.45 m to the nearest cm.
More complex relationships with direct proportion
Of course, the question in the example above could also have been answered using simple proportional reasoning, but in many cases we have to deal with less straightforward relationships; for example y might be proportional to the square of x (x²) or the cube root of x.
If ![]() and x is trebled, what happens to y?
and x is trebled, what happens to y?
Answer: ![]() becomes
becomes ![]()
… in other words, y is multiplied by 9, or 3².
What if ![]() and x is doubled?
and x is doubled?
Answer: ![]() becomes
becomes ![]()
… in other words, y is multiplied by ![]() .
.
Example 2
A sculpture consists of a set of cube-shaped blocks, each with a mass proportional to the cube of its side length. The largest block has a side length of 8 cm and a mass of 3200 g.
(a) The smallest block has a side length of 2.5 cm. What is its mass?
(b) What is the side length of a block with a mass of 400 g?
Solution
If we use M for mass and s for side length then ![]()
which gives us ![]()
We know that when s = 8, M = 3200, so substitute in those values and work out what k must be:
![]()
![]()
![]()
![]() (or
(or ![]() )
)
So the equation is ![]()
So for part (a), the smallest block, with s = 2.5, has a mass of
M = 6.25 × 2.5³ = 97.7 g (3 s.f.)
And for part (b), M = 400.![]()
![]()
![]() = 4 cm.
= 4 cm.
Your turn 1
1) In each of the expressions below,
(i) what is y directly proportional to?
(ii) identify the constant of proportionality
(iii) If x were doubled, what would happen to y?
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
2) y is directly proportional to x. When x is 42, y is 28. Write an equation of proportionality and hence find the value of (a) y when x is 77; (b) x when y = 98.
3) y is directly proportional to the square of x so that y = kx². Find the value of k and fill in the table.

4) The speed, v, of a body varies as the square root of its kinetic energy, E. When the kinetic energy is 64 joules, the speed is 27.2 m/s. What is
(a) the speed when the kinetic energy is 100 joules?
(b) the kinetic energy when the speed is 40.8 m/s?
Inverse proportion
Simple inverse proportion
y is inversely proportional to x (written in mathematical notation as ![]() ) if, when x doubles, y halves (and vice versa). “y varies inversely as x” means the same thing.
) if, when x doubles, y halves (and vice versa). “y varies inversely as x” means the same thing.
The equation (again, really a formula) looks like this:![]()
where k is a constant. Again, at Higher you’ll usually be given a pair of values for the variables and have to work out the value of the constant.
For example:
- If it takes a builder k hours to build a wall, then 3 builders will be able to do the job in a third of the time, so time is inversely proportional to number of builders. If B is the number of builders and T is the time taken then
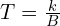
- A journey of a fixed distance of d miles takes a certain length of time if you travel at s mph. If you travel twice as fast then it will take half the time; time is inversely proportional to speed. Journey time t hours at speed s is given by
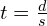 . (This is of course the distance/speed/time formula.)
. (This is of course the distance/speed/time formula.) - If substances A and B both have the same mass but B is half the volume of A, then B’s density will be twice that of A; for a given mass, density varies inversely as volume. The equation in this case is of course
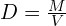 .
.
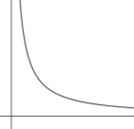
As discussed in the Foundation article, a graph showing inverse proportion looks like this – the same basic shape as the graph of ![]() . The k just stretches the graph, making it taller or wider.
. The k just stretches the graph, making it taller or wider.
Example 3
The pressure P of a given mass of gas is inversely proportional to its volume, V. Wrte down an equation for P in terms of V and find the constant of proportionality if a volume of 3 m³ has a pressure of 600 kg/m³ (600 Pa).
Hence find the pressure if the volume is reduced to 2 m³.
Solution
![]()
which gives us ![]()
We know that when V = 2, P = 600, so substitute in those values and work out what k must be:
![]()
![]()
![]()
So the equation is ![]()
and when V = 2, we have ![]() = 900 kg/m³
= 900 kg/m³
More complex relationships with inverse proportion
As with direct proportion, we sometimes have to deal with less straightforward relationships; for example y might be inversely proportional to the square of x (x²) or the cube root of x.
If ![]() and x is multiplied by 3, what happens to y?
and x is multiplied by 3, what happens to y?
Answer: ![]() becomes
becomes ![]()
… in other words, y is divided by 9 or 3².
What if ![]() and x is doubled?
and x is doubled?
Answer: ![]() becomes
becomes ![]()
![]()
… in other words, y is divided by ![]() .
.
Example 4
The force of attraction F between two magnets is inversely proportional to the square of the distance d between them. Given that, when the magnets are 2 cm apart, the force is 6 N, find
(a) the force when they are 4 cm apart
(b) how far apart they would need to be to generate a force of 15 N (answer to 3 s.f.).
Solution
![]()
which gives us ![]()
We know that when d = 2, F = 6, so substitute in those values and work out what k must be:
![]()
![]()
So the equation is ![]()
So for part (a), when d = 4![]() = 1.5 N
= 1.5 N
[Notice how d has been multipled by 2 and so F has been divided by 4 (or 2²).]
And for part (b), F = 15.![]()
![]()
![]()
![]() = 1.26 cm (3 s.f.)
= 1.26 cm (3 s.f.)
Your turn 2
1) In each of the expressions below,
(i) what is y inversely proportional to?
(ii) What is the constant of proportionality?
(iii) If x were multipled by 4, what would happen to y?
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
2) y varies inversely as x. When x is 12, y is 3. Write an equation of proportionality and hence find the value of (a) y when x is 15; (b) x when y = 5.
3) y is inversely proportional to the square of x so that ![]() . Find the value of k and fill in the table.
. Find the value of k and fill in the table.

4) In a set of shapes of length l and volume V, l is inversely proportional to the cube root of V. When l is 6 cm, V is 1000 cm³. Find:
(a) the length of the shape that has a volume of 216 cm³
(b) the volume of a shape with a length of 12 cm.
Together with the article covering the Foundation material, that covers the topic of direct and inverse proportion for GCSE Maths. I hope you’ve found it helpful.
If you’ve found this article helpful then please share it with anyone else who you think would benefit (use the social sharing buttons if you like). If you have any suggestions for improvement or other topics that you’d like to see covered, then please comment below or drop me a line using my contact form.
On my sister site at at mathscourses.co.uk you can find – among other things – a great-value suite of courses covering the entire GCSE (and Edexcel IGCSE) Foundation content, and the “Flying Start to A-level Maths” course for those who want to get top grades at GCSE and hit the ground running at A-level – please take a look!
If you’d like to be kept up to date with my new content then please sign up to my mailing list using the form at the bottom of this page, which will also give you access to my collection of free downloads.
Answers: Your turn 1
1) (a) ![]() ; k = 9; ×2
; k = 9; ×2
(b) ![]() ; k = 3; ×2²
; k = 3; ×2²
(c) ![]() ; k =
; k = ![]() or 0.4; ×
or 0.4; ×![]()
(d) Square root both sides to make y the subject so ![]() ; k = 3; ×
; k = 3; ×![]()
2) ![]() ; (a) y = 44; (b) x = 56
; (a) y = 44; (b) x = 56
3) k = 7

4) k = 3.4; (a) 34 m/s; (b) 144 J
Click here to return to questions
Answers: Your turn 2
1) (a) x; k = 3; ÷4
(b) x²; k = 5; ÷4²
(c) ![]() ; k =
; k = ![]() or 1.8; ÷
or 1.8; ÷![]()
(d) Square root both sides to make y the subject so y is inversely proportional to ![]() ; k = 4; ÷
; k = 4; ÷![]() , i.e. ÷2
, i.e. ÷2
2) ![]() ; (a) y = 2.4; (b) x = 7.2
; (a) y = 2.4; (b) x = 7.2
3) k = 900

4) ![]() ; (a) 10 cm; (b) 125 cm³
; (a) 10 cm; (b) 125 cm³