What’s the difference between GCSE and IGCSE Maths?

Are you unclear on how GCSE and IGCSE Maths differ from each other? This article aims to help you understand the differences between the English GCSE Maths qualification and the Edexcel International GCSE.

Note: The Cambridge IGCSE, although briefly mentioned, is not included in this comparison.

Introduction

The GCSE (General Certificate of Secondary Education) is the standard Maths qualification taken at age 16 (the end of Year 11) by students in English state schools and some independent schools. The specification is prescribed by Ofqual, the Government agency in charge of qualifications, and is nominally the same across all the exam boards that offer it, although there are some minor differences in interpretation.

The main exam boards for GCSE Maths are AQA (specification code 8300), Edexcel (1MA1) and OCR (J560).

The Edexcel International GCSE (Specification A; code 4MA1) cannot be offered in state schools as it is not regulated in the same way, but many independent schools choose to offer it instead of the GCSE, as there is some perception that it’s slightly easier. In terms of access to A-level and other Level 3 courses, it is normally regarded as being equivalent.

Edexcel also offer a Specification B qualification (code 4MB1) which is available at Higher Tier only and includes some different topics such as matrices. Since matrices aren’t in the English A-level Maths specification, I believe that Spec B is aimed more at overseas institutions – perhaps those offering the International Baccalaureate in lieu of A-levels? Personally I’ve only encountered Spec A and so that’s what the content of this article is based on.

The IGCSE papers are more formulaic and predictable than those for GCSE. This is partly because the IGCSE is written with non-native English speakers in mind and so the wording is kept as simple as possible. It could, of course, also be argued that Pearson (who own Edexcel) keep it slightly easier to boost uptake!

There is also a Cambridge IGCSE with two variants (0580 and 0980) – in fact Cambridge holds the trademark for the “IGCSE” name and so, strictly speaking, it shouldn’t really be used to refer to the Edexcel qualification; you won’t see Edexcel themselves calling their own qualitification “IGCSE”, though the abbreviation is in common use generally. Unfortunately I’m not sufficiently familiar with the Cambridge specifications to comment on them, except to say that they are primarily used by overseas schools. Any further mention of IGCSE in this article refers to the Edexcel International GCSE Specification A, as taught in many independent schools in England.

Exam format

Both GCSE and IGCSE are graded from 1 to 9 – with 9 being the top grade – and have the option of a Foundation or a Higher Tier. On Foundation it’s possible to achieve up to a Grade 5; Grade 4 is a Level 2 pass, equivalent to a Grade C on the old scale. (Grades 1-3 are a Level 1 pass.) On Higher Tier you can get Grades 4 to 9… or a U, which is a fail. If you’re doing Higher Tier and only just miss a Grade 4 then you may be awarded a 3 – effectively a “nearly a pass” grade.

So you should only take the Higher Tier if you can confidently expect to get at least a Grade 4 and are really aiming for 6 or above. Approximately 50% of the marks on the Higher paper are aimed at candidates aspiring to Grade 7 and above (this is the usual requirement for entry to an A-level Maths course), so most of a Higher paper will be inaccessible to someone who’s doubtful of achieving Grade 4.

Both GCSE and IGCSE are entirely exam-based; there is no coursework element in either qualification.

The GCSE exam consists of three papers, all the same Tier and each 90 minutes in length. For AQA and Edexcel, Paper 1 must be completed without the use of a calculator, but calculators are allowed for Papers 2 and 3. For OCR it’s Paper 2 that’s non-calculator. (For information on which calculators are appropriate for both the GCSE and IGCSE exams, take a look at my Clueless about Calculators? blog post.) The main GCSE exam sitting is in May/June, with a resit opportunity in November.

The IGCSE exam (4MA1) consists of only two papers, each of 2 hours in duration and normally sat at the same time as GCSE Papers 1 and 2. Again, you can’t mix Tiers. A calculator is permitted for both papers. Until 2023, the Edexcel IGCSE could also be taken in January, but starting in November 2023 it’s been brought into line with the other exam boards, with sittings in November and May/June.

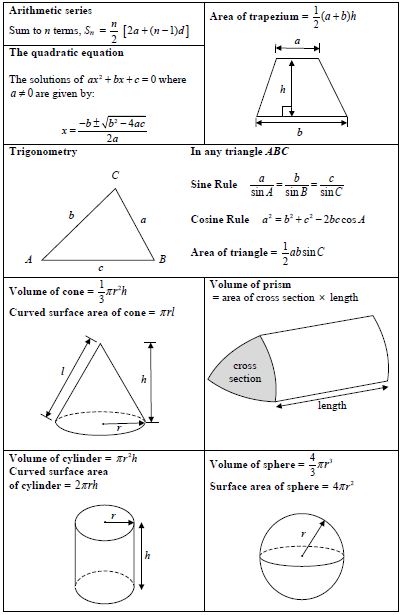
For GCSE, the student is expected to learn most of the necessary formulae, but for IGCSE, a formula sheet is provided at the front of the paper.

Differences in content: Foundation

The differences between the the GCSE and IGCSE at Foundation level are fairly minimal.

You can find the Ofqual GCSE specification for both Foundation and Higher Tiers here (see the subject content section; underlined skills are required for Foundation, and the rest for Higher), though the exam board specifications linked above also provide the same information.

For Foundation Tier, the topics/skills that are in GCSE but not IGCSE are:

• error intervals
• inverse proportion (in Higher Tier for IGCSE)
• systematic listing strategies
• sequences: geometric, triangular numbers, square numbers, Fibonacci sequence
• criteria for congruence
• exact trig values for special angles
• loci
• constructing a perpendicular from a point to a line
• class interval containing the median
• 2-way tables
• bivariate data / scatter graphs / correlation
• stem & leaf diagrams (not explicitly on Ofqual GCSE spec but Edexcel includes it)

and in IGCSE but not GCSE:

• linear inequality graphs (shading regions)
• rate of change and tangent to a graph

(These are both in the GCSE but only the Higher Tier.)

Differences in content: Higher

The differences here are more significant.

For Higher Tier, the topics/skills that are in GCSE but not IGCSE are:

• geometric sequences
• nth term of a quadratic sequence
• exponential functions and exponential growth
• equation of a circle and of the tangent to a circle at a given point
• finding the area under a graph
• using iteration to find approximate solution to an equation
• systematic listing strategies: product rule of counting
• proofs of circle theorems
• frustum of a cone
• box plots (box-and-whisker diagrams)
• enlargement with a negative scale factor

and in IGCSE but not GCSE:

• intersecting chords theorem (in circle theorems)
• modulus of a vector
• sum of the first n terms of an arithmetic series
• understanding domain and range
• differentiation with positive and negative (but not fractional) indices
• using differentiation to find gradients and stationary points on a curve
• optimisation problems using differentiation
• applying differentiation to linear kinematics problems (displacement, velocity, acceleration)

Well, that’s it – I hope you’ve found this summary helpful. If you have any comments on this article, or requests for topics that you’d like me to cover in future posts, then please comment below!