Working with factors and multiples, HCF and LCM

Factors and multiples have a wide variety of uses in many different areas of Maths, so it’s a fundamental topic that you need to have a good grasp of.

In this post we’ll look at how to identify a number’s factors and multiples, and how to find the HCF (highest common factor) and LCM (lowest common multiple) of two or more numbers.

The next post, which you can find here, looks at situations and types of exam questions where you need to use skills involving factors and multiples.

What are factors and multiples?

A lot of people get confused between factors and multiples, but it’s important that you know which is which.

A multiple of a number N is what you get why you multiply N by another (whole) number. In other words, it’s a number in the N times table. Since a times table can go on for ever, the number of multiples of N is unlimited.

So the first few multiples of 8, for example, are 8, 16, 24, 32, 40… and so on.

In some cases you can use the rules of divisibility to help you work out whether one number is a multiple of another.

A factor of N is a number that N is divisible by; in other words, N is a number in the factor’s times table. A number only has a limited number of factors.

So the factors of 8, for example, are 1, 2, 4 and 8.

How to list all the factors of a number

Sometimes you’ll be asked to list the factors of a number, sometimes you’ll need to express the number as a product of its prime factors. Let’s look at the list of factors first.

Start with 1 × the number itself.

Then below that, write the next factor up from 1 (if the number is even then the next factor will be 2), alongside the other factor that you need to multiply it by to make the original number.

Repeat this process so that you end up with the left-hand column counting up and the right-hand column counting down, until they meet in the middle.

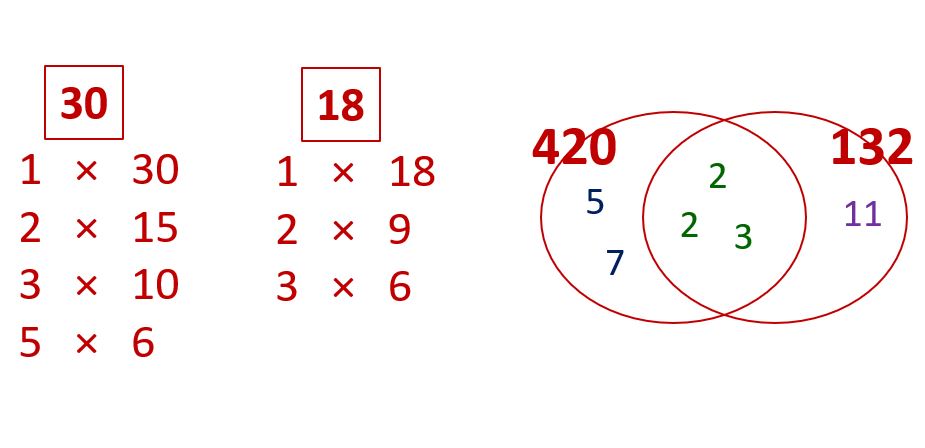
Here’s an example, finding the factors of 30:

(4 is omitted from the left-hand column because it isn’t a factor of 30.)

Notice that going from 1 to 2 means you’re doubling the first factor, and at the same time going from 30 to 15 is halving the second factor, so it balances out; you could think of the 2 × 15 as being 1×2 × 30÷2.

Similarly, going from 1 to 3 you’re multiplying by 3, and that’s balanced by the other factor (going from 30 to 10) being divided by 3.

Sometimes this can help you to work out unknown factors.
For example, 52 can be written as 1 × 52;
double the 1 and halve the 52 to get 2 × 26;
3 isn’t a factor (the digits don’t add up to a multiple of 3 – see this post on rules of divisibility)
double the 2 to get 4 and halve the 26 to get 13 so we have 4 × 13.

Your turn 1: Listing factors and multiples

1. List the first five multiples of (a) 6; (b) 15
2. List all the factors of (a) 15; (b) 42; (c) 72

Check your answers here.

Product of prime factors using a factor tree

Any positive integer is also the product of a set of prime factors (i.e. factors that are prime numbers). No two numbers have the same set of prime factors.

The process of breaking a number down into its prime factors is sometimes referred to as “prime factor decomposition”.

To express a number as a product of its prime factors, use a factor tree. You start at the top, with the number you’re breaking down. Split it into a pair of its factors – it doesn’t matter which pair, as long as multiplying them together gives you the original number.

If one of the factors you’ve chosen is a prime number then circle it; that’s the end of that branch.

Now split any remaining (non-prime) factors into factor pairs; circle any prime factors you find, and carry on breaking down any factors that aren’t prime numbers until every branch ends in a prime number.

Finally, express the original number as a product of all the prime factors you’ve identified.

Example: Here’s a factor tree showing one possible way of breaking down 420. We’ve started with 10 × 42, but we could equally well have used 2 × 210 or 20 × 21; they’d all have given the same result in the end. Try it with some different factor pairs if you like!

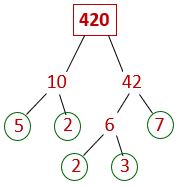
Neither 10 nor 42 is prime so we had to break them both down further: 10 into 5 and 2, and 42 into 6 and 7. That gave us prime factors 5, 2 and 7, but one more step was needed to break down the 6.

You can see that the prime factors we’ve ended up with are 5, 2, 2, 3, 7…
so we can express 420 as a product of its prime factors like this:

420 = 2 × 2 × 3 × 5 × 7

or in index form:

420 = 2² × 3 × 5 × 7

If you take any combination of these prime factors and multiply them together then the product will be a factor of 420.
For example, 2 × 3 × 5 = 30, and 2 × 7 = 14
and 30 × 14 = 420.

Conversely, any number that has prime factors not in the list is not a factor of the original number.
For example, 8 = 2 × 2 × 2 and there are only two 2s in the prime factors of 420, so 8 is not a factor of 420 (but 4 is).

You can also use a calculator to obtain the prime factorisation of a number using the FACT function. On a Casio, put the number in, press = then SHIFT and then the deg/min/sec button (which has FACT above it).
If the display doesn’t change then it must already be a prime number.

Your turn 2: Listing prime factors

1. Use factor trees to express these numbers as products of their prime factors in index form:
   (a) 45
   (b) 72
   (c) 280
2. Use your prime factor list for 280 to decide whether the following are factors of 280:
   (a) 4
   (b) 6
   (c) 16
   (d) 35

Click here for answers (or check using your calculator).

What’s the HCF and how can I find it?

The HCF of a pair (or set) of numbers is the highest common factor – i.e. the biggest number that is a factor of both (or all) of the numbers.

One way to find an HCF is to list all the factor pairs for each number and work your way down the list, starting with the biggest factor, until you find a factor that appears in both (or all) the lists.

Example: The factors of 30 and 18 are listed below. Start with the biggest number in the shorter list, i.e. the factors of 18 (it doesn’t really matter which list you start with, but it’s usually quicker if you pick the shorter one):

18 doesn’t appear in the list for 30 so it’s not a common factor.
9 doesn’t appear in the list for 30 so it’s not a common factor.
6 is the biggest number that appears in both lists so the HCF of 30 and 18 is 6.

What’s the LCM and how can I find it?

The LCM of a pair (or set) of numbers is the lowest common multiple – i.e. the smallest number that appears in both (or all) of their times tables.

One way to identify the LCM of a pair (or set) of numbers is to write out the first few multiples of each number until you find the first one that occurs in both (or all) lists.

Example: To find the LCM of 9 and 12, list the first few multiples of 9 and 12:
9, 18, 27, 36, 45, …
12, 24, 36, …

The first number that appears in both lists is 36, so the LCM of 9 and 12 is 36.

Your turn 3: Finding HCF and LCM by comparing lists

1. Use the lists of factors that you made earlier to find the HCF of
   (a) 30 and 42
   (b) 15, 42 and 72
2. Find the LCM of
   (a) 12 and 16
   (b) 10 and 16
   (c) 8, 10 and 15

Click here for answers

Using a Venn diagram to identify HCF and LCM

Another method that you can use to find both the HCF and the LCM of a pair (or set of three) numbers is a Venn digram. This method is especially useful for larger numbers.

First, you need to decompose each number into its prime factors.

Once you’ve done that, draw a Venn diagram with a circle for each number and put the prime factors in the appropriate sections. It may help you to keep track if you cross the numbers off as you place them in the Venn diagram – remembering to cross them off everywhere that they occur.

Example: 420 = 2 × 2 × 3 × 5 × 7 and 132 = 2 × 2 × 3 × 11

Both sets of factors contain two 2s and one 3 so those go in the overlap, and the remaining factors go into the exclusive sections of their respective circles, like this:

You can find the HCF by multiplying together the prime factors in the overlap:

HCF of 420 and 132 = 2 × 2 × 3 = 12

… and you can find the LCM by multiplying together all the numbers in both circles – or, more quickly, by taking one of the original numbers and multiplying it by the numbers in the other circle(s) (which amounts to the same thing since, as you already know, the first number is the product of all the prime factors in its circle):

LCM of 420 and 132 = 2 × 2 × 3 × 5 × 7 × 11
OR 420 × 11
OR 132 × 5 × 7
= 4620

Your turn 4: HCF and LCM using Venn diagrams

Draw a Venn diagram for each set of numbers and use it to find the HCF and LCM of

1. 30 and 42
2. 16 and 36
3. 15, 42 and 72

Click here for answers

That covers the definitions and skills that you need for working with factors and multiples, HCF and LCM.

In the next post, which you can find here, I cover a wide range of the types of problems where these skills will be useful.

---

Answers

Your turn 1: Listing factors and multiples

1. (a) 6, 12, 18, 24, 30
   (b) 15, 30, 45, 60, 75
2. (a) 1, 3, 5, 15
   (b) 1, 2, 3, 6, 7, 14, 21, 42
   (c) 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 3, 72

Back to this section

Your turn 2: Prime factor trees

1. (a) 45 = 3² × 5
   (b) 72 = 2³ × 3²
   (c) 280 = 2³ × 5 × 7
2. (a) 4 = 2 × 2 and these are both factors of 280 so yes, it’s a factor
   (b) 6 = 2 × 3 and 3 isn’t a factor of 280 so no, it’s not a factor
   (c) 16 = 2⁴ or 2×2×2×2 but the factor of 2 only occurs 3 times in 280 so no, not a factor
   (d) 35 = 5 × 7, both factors of 280 so yes, it’s a factor.

Back to this section

Your turn 3: Finding HCF and LCM by comparing lists

1. (a) 6, (b) 3
2. (a) 48, (b) 80, (c) 120

Back to section on HCF / Back to section on LCM

Your turn 4: HCF and LCM using Venn diagrams

1. HCF = 6, LCM = 210
2. HCF = 4, LCM = 144
3. HCF = 3, LCM = 2520

Back to this section