Factors, multiples, HCF and LCM questions and problems

In this post we’ll look at HCF and LCM questions, and other situations and types of problems where you need to use what you know about factors and multiples. They start off pretty straightforward, then go on to word problems given in context, and we finish off with some trickier problems involving prime factors, HCF and LCM, aimed mainly at those targeting high grades.

This article follows on from “Working with factors and multiples, HCF and LCM“, which explains the meanings of the terms factor, multiple, HCF and LCM, and shows you to find them. If you’re not confident with these skills then you’ll find it helpful to work through that post before looking at this one.

Basic questions on factors and multiples

The more straightforward question types were all covered in the previous article, so they shouldn’t require any further explanation. Have a go at the questions below, and go back and look at the previous article if there are any that you struggle with.

1. List the first four multiples of 6.
2. What is the fifth multiple of 4?
3. List all the factors of 24.
4. How many factors does 36 have?
5. Identify from the list of numbers
   2, 5, 6, 12, 20, 27, 30, 36
   (a) all the factors of 60;
   (b) all the multiples of 12;
   (c) a factor of 30 that is not also a multiple of 2.
6. Express 360 as a product of its prime factors in index form.
7. Find the highest common factor of 24 and 42.
8. Find the lowest common multiple of 24 and 42.
9. By drawing a Venn diagram, find the HCF and LCM of 36, 56 and 84.

Click here for answers

Identifying common factors is also an essential skill for:

Cancelling fractions: To cancel down a fraction, you need to divide by the same number top and bottom. It doesn’t have to be the HCF – you can do it in several steps if you like – but if you can spot the HCF then you can cancel the fraction down to its simplest terms in a single step.

Factorising: To fully factorise an algebraic expression, you need to take the HCF outside the bracket. In this context, the HCF can include letters as well as numbers.
For example:
1. The HCF of 7a + 8ab
is a
so the factorised form is a(7 + 8b).
2. The HCF of 12x²y³ – 18 x²y
is 6x²y
so the factorised form is 6x²y(2y² – 3).

Contextual (word) problems

These types of questions involve finding either an HCF or an LCM in order to solve a word problem. They often involve contexts such as buying packs of burgers and buns, or flashing lights, or buses.

Example 1
The Number 9 bus comes every 9 minutes and the Number 12 bus comes every 12 minutes. If both buses arrive at exactly 8:00, what is the first time they will both arrive together after 9:00?

Solution:
It’s a “coinciding” question so we need the LCM.
The LCM of 9 and 12 is 36, so the buses will both arrive at the same time after every 36 minutes.
One lot of 36 minutes only takes us to 8:36 so we need another 36 minutes, which will take us to 9:12.

Example 2:
Alex wants to tile a section of wall measuring 2.40 m high × 3.15 m wide, using square tiles. What is the largest tile size she can use without having to cut any to size, and how many tiles will she need? (Assume that there are no gaps between the tiles.)

Solution:
Here we’re dividing the wall up into tiles, so we need the HCF.
Use centimetres to make the numbers easier, so we’re working with 240 and 315.
Break each number down into its prime factors and use a Venn diagram to find the HCF:

HCF of 240 and 315 = 3 × 5 = 15
So maximum tile size = 15 cm on each side.

For the number of tiles needed, you can either work out the area of the whole wall and divide by the area of a single tile, or work out how many will fit in each direction, like this:

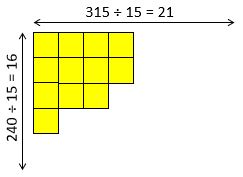
You need 21 tiles horizontally and 16 vertically,
so the total number of tiles required is 21 × 16 = 336.

Your turn 1: Contextual questions

1. KissFM gave a £50 note to every 50th caller. Every 40th caller received free concert tickets. How many callers had to get through before one of them received both cash and concert tickets?
2. Rosa is making a game board that is 16 inches by 24 inches. She wants to use square tiles. What is the largest tile she can use, and how many tiles will she need?
3. Two bikers are riding a circular path. The first rider completes a round in 12 minutes. The second rider completes a round in 18 minutes. If they both started at the same place and time and go in the same direction, after how many minutes will they meet again at the starting point?
4. Sean has 8-inch pieces of toy train track and Ruth has 18-inch pieces of train track. How many of each piece would each child need to build tracks that are equal in length?
5. I am planting 50 apple trees and 30 plum trees. I want the same number of trees in each row, and only one type in each row. What is the maximum number of trees I can plant per row?
6. Jim hits his drum every 8 beats, Tim taps his tambourine every 10 and Kim clashes her cymbals every 12. They all sound their instruments together. How many beats before they do so again?
7. Sam has two pieces of cloth, one 144 cm wide and the other 96 cm wide. She wants to cut both into equal strips that are as wide as possible, with none left over. What’s the widest strip width she can cut?
8. You’re catering for an event and need to provide at least 100 sandwiches, each consisting of a roll and a slice of ham. Rolls come in packs of 8, each costing £1.20, and ham slices in packs of 12, each costing £3.50. You don’t want to have any rolls or ham slices left over. What’s the minimum spend required?

Click here for answers

Tricky prime factor, HCF and LCM questions

Here are some examples of harder questions that, in theory, could appear on Foundation papers, but are more likely to come up only on Higher papers.

Example 1:
Given that d = 2³ × 7, express 10d as a product of its prime factors.

Solution:
You don’t actually need to find d!
The prime factors of 10 are 2 and 5, so 10d = 2 × 5 × 2³ × 7.
Tidy this up to give 10d = 2⁴ × 5 × 7.

Example 2:
By finding its prime factors, identify the square root of 7056.

Solution:
As a product of its prime factors, 7056 = 2⁴ × 3² × 7².
This can be written as 2²×3×7 × 2²×3×7 or (2²×3×7)²
So the square root of 7056 is 2²×3×7 = 84.
(A square number will always have a repeated set of prime factors.)

Example 3:
Without using a calculator, find the least number by which 1980 can be multiplied to give a square number, and identify the square root of that number.

Solution:
As in the previous example, for a number to be a square number, it needs a repeated set of prime factors.
The prime factors of 1980 are 2, 2, 3, 3, 5 and 11.
To give a repeated set we need to multiply by another 5 and another 11
so the least number by which the 1980 can be multiplied is 5 × 11 = 55.
The square root of the resulting square number (which is 1980 × 55 =108900)
will be 2 × 3 × 5 × 11 = 330.

Example 4:
Find the greatest number which divides into 167 and 95 leaving 5 as remainder.
(i.e. Divide either 167 or 95 by this number and the remainder will be 5.)

Solution:
If the remainder is 5 then the number must be a factor of 167 – 5 and of 95 – 5
so the number we’re looking for is the HCF of 162 and 90.
162 = 2 × 3⁴ and 90 = 2 × 3² × 5
so the number is the overlap of these, i.e. 2 × 3² = 18.

Example 5:
Find the smallest number which leaves 5 as a remainder when divided by 95 or 114.

Solution:
The number we’re looking for must be 5 more than the LCM of 95 and 114.
95 = 5 × 19 and 114 = 2 × 3 × 19
so LCM = 2 × 3 × 5 × 19 = 570
Hence the number must be 570 + 5 = 575.

Example 6:
Find a pair of 2-digit numbers with an HCF of 6 and an LCM of 168.

Solution:
The prime factors of 6 are 2 × 3, and of 168 are 2³ × 3 × 7.
The HCF of 2 × 3 (or simply 6) goes in the overlap on the Venn diagram.
Then you need to distribute the remaining 2, 2, and 7 between the exclusive parts of the circles:

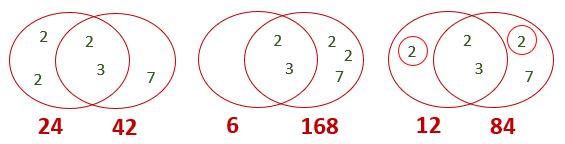
Note, however, that the third option shown above doesn’t work, because you can’t have the same number in the exclusive parts of both circles; if 2 is in A but not in B, then it can’t also be in B but not in A! In fact 12 and 84 have an HCF of 12 and an LCM of 84, rather than the 6 and 168 specified in the question.

Of course 6 and 168 aren’t 2-digit numbers, so the only possible solution is 24 and 42.

Your turn 2: Tricky questions

1. Given that a = 2 × 3² × b, where b is a prime number greater than 10, express 5ab in terms of b.
2. Use prime factor decomposition to identify
   (a) the square root of 69696
   (b) the cube root of 74088
3. Write 1008 as the product of prime factors, and hence find the least number that 1008 needs to be multiplied by to give a square number.
4. Find the smallest square number of which 350 is a factor.
5. Find the largest number that divides by 317 and 227 leaving 2 as remainder.
6. Find the smallest number which, on 23 being added to it, is exactly divisible by 32, 36, 48 and 96.
7. The product of two numbers is 2160. If their HCF is 6,  what is their LCM?
8. Find a pair of 3-digit numbers with 45 as their HCF and 2970 as their LCM.
9. Two numbers 72 and n have HCF = 12 and LCM = 504. What is n?
10. Three numbers, 42, 63 and x have HCF = 21 and LCM = 630. What are the four possible values of x?

Click here for answers

That’s it for this collection of prime factor, HCF and LCM questions. For more practice, take a look at videos 218, 219 and 22 (and the associated question packs) on Corbettmaths, and the relevant “Grade 4” content on MathsGenie.

---

Answers

Basic questions

1. 6, 12, 18, 24
2. 20
3. 1, 2, 3, 4, 6, 8, 12, 24
4. 9 (the 6 is repeated)
5. (a) 2, 5, 6, 12, 20, 30; (b) 12, 36; (c) 5
6. 360 = 2³ × 3² × 5
7. 7. HCF = 6
8. LCM = 168
9. HCF = 4, LCM = 504

Back to this section

Your turn 1: Contextual questions

1. LCM = 200 callers
2. HCF = 8 inches, so 2 x 3 = 6 tiles of side length 8 inches
3. LCM = 36 mins
4. LCM = 72 cm, so 9 pieces for Sean and 4 pieces for Ruth
5. HCF = 10 trees
6. LCM = 120 beats
7. HCF = 48 cm
8. LCM = 24 but need 5 × 24 = 120 of each. That’s 120 ÷ 8 = 15 packs of rolls @ £1.20, and 120 ÷ 12 = 12 packs of ham @ £3.50, giving a total cost of £53.00.

Back to this section

Your turn 2: Tricky problems

1. 5ab = 5 × 2×3²×b × b = 2 × 3² × 5 × b²
2. (a) 2³×3×11 = 264; (b) 2×3×7 = 42
3. 1008 = 2⁴×3²×7; multiply by 7 (to give 7056)
4. 350 = 2×5²×7; multiply by 2 and 7 to get 4900
5. HCF of 315 and 225 = 45
6. Need to find LCM of all these, then minus 23. Can ignore 32 and 48 since they are factors of 96. LCM of 36 & 96 = 288, and 288 – 23 = 265
7. 360
8. 270 and 495, or 135 and 990
9. 84
10. 105, 210, 315, 630

Back to this section