What does “Integration as the limit of a sum” mean?
The English A-level Maths specification includes “integration as the limit of a sum” and “Fundamental Theorem of Calculus”. This article explains these expressions.
Using strips to estimate the area under a curve
To estimate the area under a curve, we divide the area under the curve into a series of strips and add all their areas together.
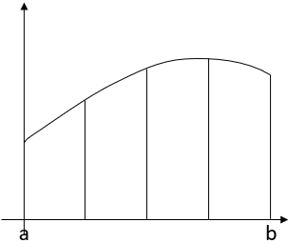
The area under this curve between a and b has been divided into 4 strips. We can approximate the shapes of the strips to rectangles or trapezia; for simplicity in this case, let’s use rectangles, each the same height as the left-hand side of the strip.
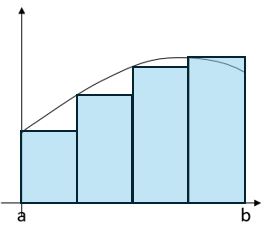
As you can see, the sum of the areas of all the strips is less than the area under the curve, so this approach will give us an underestimate of the actual area. (The last two strips looks as if they’ll roughly cancel out, since one is under the curve and the other is over by about the same amount, but the first two are both well below the curve.)
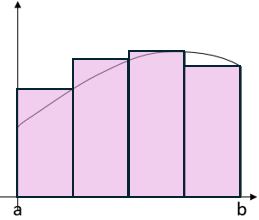
If we use the right-hand side of each strip instead then we get this, which of course is an overestimate:
Side note: If an exam question asks you to show that the area under a curve is between two given values, this principle is what they expect you to use.
The whole of the section of curve you are given will probably have either a positive or a negative gradient, so that you consistently get either an underestimate or an overestimate from every strip for its part of the curve. Therefore using one side of each rectangle will give you a value that you know is less than the actual area, and using the other side will give you one that’s more than the actual area.
Hence the actual area must lie between these two extremities.
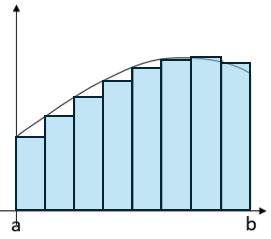
If the width of each strip is δx (the lowercase delta denotes a small change so this means “a small change in x”) and the height of strip n is 
, then the estimate of the area under the curve can be expressed as the sum of the areas of the strips, i.e. 
… which can also be written as
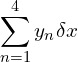
(where the Greek capital letter sigma, Σ, represents the sum of a set of discrete values).
Improving the accuracy
In this version of the same graph, we’ve split the area into 8 strips.
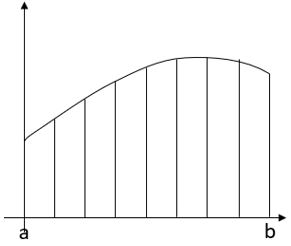
Drawing in the rectangles again, you can see that the gaps between the tops of the rectangles and the curve are much reduced, so the accuracy of our estimate has improved.
The more strips we have, the closer we’ll get to the actual area.
Increasing the number of strips improves the accuracy of the estimate.
(This statement might get you a mark in a trapezium rule question!)
The limit of a sum / Fundamental Theorem of Calculus
As we get to the stage of having so many strips that the width of each strip approaches zero, the sum of the areas of the strips will become indistinguishable from the actual area under the graph. (Of course, if the width is actually zero then the area is also zero so we can’t go that far!)
So the actual area under the curve is given by
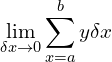
i.e. the limit of the sum of the areas of a very large number of strips, each of width approaching zero…
… and since we are now dealing with a continuous function rather than a set of discrete values, this can also be represented by the more familiar
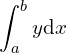
This concept – that the sum of the areas of a series of infinitely narrow strips is the same as the area under the curve – is what’s known as the Fundamental Theorem of Calculus.
Example exam-style question
Questions written to test your understanding of “integration as the limit of a sum” or “the Fundamental Theorem of Calculus” are likely to look something like this:
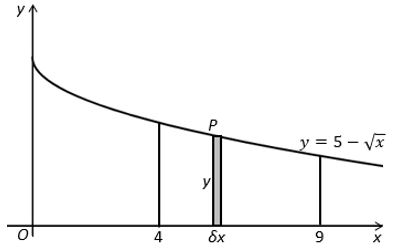
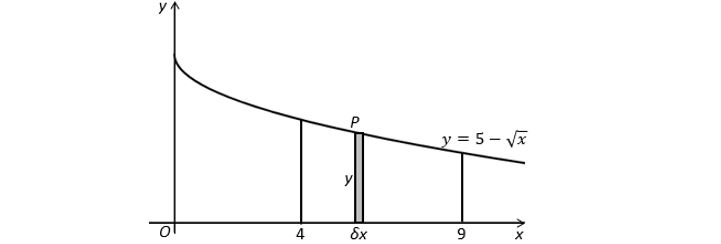
The graph of 
is shown in the figure above.
The point P (x, y) lies on the curve.
The shaded rectangle has height y and width δx.
Calculate
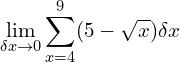
Now that you know what the sigma expression means, it’s dead simple! Just find the integral of 
between 4 and 9.
(You should get an answer of 
.)
Well, that about covers it. I hope that the expressions “integration as the limit of a sum” and “Fundamental Theorem of Calculus” mean a little more to you now than they did before you read this article!
If you’ve found this article helpful then please share it with anyone else who you think would benefit (use the social sharing buttons if you like). If you have any suggestions for improvement or other topics that you’d like to see covered, then please comment below or drop me a line using my contact form.
On my sister site at at mathscourses.co.uk you can find – among other things – a great-value suite of courses covering the entire GCSE (and Edexcel IGCSE) Foundation content, and the “Flying Start to A-level Maths” course for those who want to get top grades at GCSE and hit the ground running at A-level – please take a look!
If you’d like to be kept up to date with my new content then please sign up to my mailing list using the form at the bottom of this page, which will also give you access to my collection of free downloads.
