Direct and inverse proportion for Foundation GCSE

For Foundation GCSE you need to know what equations and graph shapes represent direct and inverse proportion, and work with equations given to you, but you don’t have to actually derive the equations, as you do at Higher.

You also need the Foundation content covered here if you’re doing Higher Tier, but if you want to go straight to the Higher content then you can find that here.

The “Direct and inverse proportion” lesson on this page is based on an extract from the Algebra module of my Grade 4 Essentials course – ideal for anyone who’s doing Foundation GCSE and doesn’t want to get confused by Higher content that they don’t need! The four main modules cover all the skills you need for a secure Grade 4, and there’s an additional “Top-end Topics” extension module for anyone who’s aiming for a Grade 5 or is doing Higher and wants to make sure that they’ve got all the Foundation content sussed.

The course is great value for money, and there are even discounts to be had – as well as some useful free downloads – if you sign up to my mailing list using the form on my home page or in the footer of any page on this site.

You can download a printable PDF version of this post here (you might find it useful for answering the graph questions).

Direct proportion

y is directly proportional to x (written in mathematical notation as ) if, when x doubles, y doubles. If x is multiplied by 10 then y is also multiplied by 10; if x is halved then so is y.

The equation (really it’s a formula, since there are two variables) looks like this:

where k is a constant. At Higher Tier you usually have to work out the value of the constant, but at Foundation it will be given if you need it. Note that k might be a fraction, so the equation might look like, for example, .

For example:

• If it takes a decorator 3 hours to decorate one room, then the time T taken to decorate more than one room will be the 3 hours multiplied by the number of rooms, n, giving T = 3n
• If it costs 129p for 1 litre of fuel then V litres will cost V x 129, giving a total cost (in pence) of C = 129V

A graph showing direct proportion is a straight-line graph with a positive gradient that goes through the origin. (It can go into negative values but it usually just starts from 0.) For example, the graph for fuel at 129p/litre would look like this:

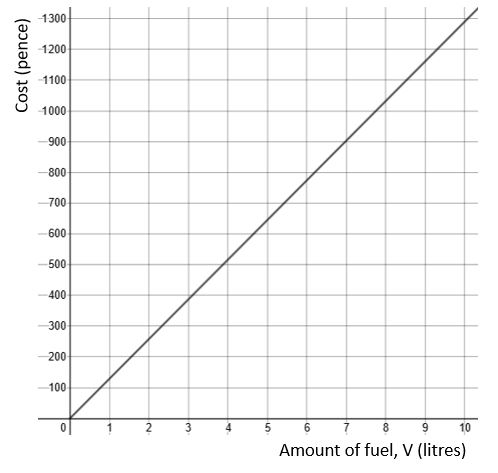
Conversion graphs often look like this too; for example with currency conversions, if you double the amount in pounds then that doubles the value in dollars too. Similar for metric-imperial conversions, e.g. between kg and pounds, or between miles and km.

You can use a graph like this to read off values.

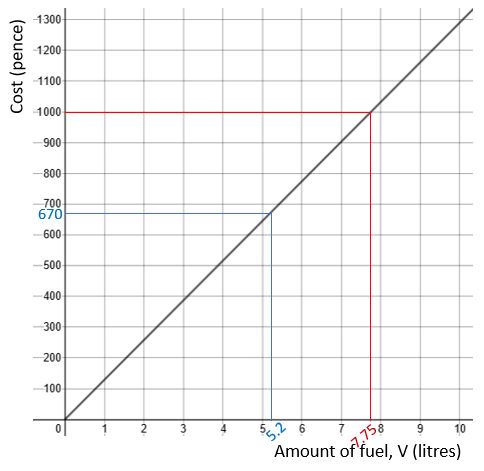
See if you can use the graph above to estimate the cost of 5.2 litres of fuel. Do this by finding 5.2 on the horizontal (amount of fuel) axis, drawing a line straight up to the graph and then across to the vertical (cost) axis.

Now use the graph to estimate how much fuel you could buy for £10.00. Again, draw lines on the graph. Don’t forget that you need to turn the £10.00 into pence first!

You’ll find the answers a little further down this page.

Now work out the same answers using the formula C = 129V. Your answers should match, though of course the calculation method will give a greater degree of accuracy.

Cost of 5.2 litres:
C = 129V and V = 5.2 litres
C = 129 x amount of fuel =129 x 5.2 = 670.8 p = £6.71 to the nearest penny.
By reading it off the graph you’ll probably have got a value between £6.60 and £6.80 – see blue lines on image below.

Amount of fuel for £10.00:
C = 1000 pence and we need to find V
We have 1000 = 129V
so V = 1000 ÷ 129 = 7.75 litres (3 s.f.)
By reading it off the graph you’ll probably have got a value between 7.7 and 7.8 litres – see red lines on image below.

Inverse proportion

y is inversely proportional to x (written in mathematical notation as ) if, when x doubles, y halves (and vice versa).

The equation (again, really a formula) looks like this:

where k is a constant. Again, at Higher you usually have to work out the value of the constant, but at Foundation it will be given if you need it.

For example:

• If it takes a builder 12 hours to build a wall, then 3 builders will be able to do the job in a third of the time. If B is the number of builders and T is the time taken then  
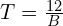
• A journey of 70 miles takes a certain length of time if you travel at 30 mph. If you travel twice as fast then it will take half the time. Journey time t hours at speed s is given by 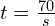. Can you see how this relates to the distance/speed/time formula?
• If substances A and B both have the same mass but B is half the volume of A, then B’s density will be twice that of A. The equation in this case is of course .

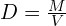A graph showing inverse proportion looks like this – the same basic shape as the graph of . The k just stretches the graph, making it taller or wider.

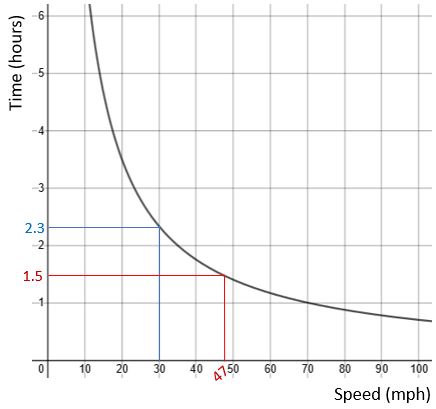
For example, here is the graph for the 70-mile journey described above.

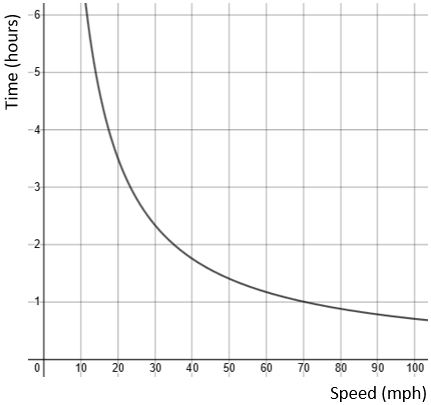
Use the graph to estimate how long the journey would take if you travelled at 30mph. (Draw lines on it as you did before, this time up from 30 mph and then across to the time axis.)

Now use the graph to estimate what average speed you’d have to travel at to complete the trip in 1½ hours.

You’ll find the answers a little further down this page.

Now work out the same answers using the formula . Again, you should get the same answers, though the calculated values will be to a greater degree of accuracy.

Journey time at 30 mph:
and s = 30
hours = 2 hours 20 minutes
(You can use the [° ‘ “] button on your calculator to convert 2.33333… hours to hours and minutes – and seconds if applicable.)
By reading it off the graph you’ll probably have got a value between 2.25 and 2.4 hours – see blue lines on image below.

Speed needed to complete the trip in 1½ hours:
t = 1.5 and we need to find s
We have
Multiply both sides by s to get
Then divide both sides by 1.5 to get = 46.7 mph (3 s.f.)
By reading it off the graph you’ll probably have got a value between 45 and 48 mph – see red lines on image below.

And that’s everything you need to know about direct and inverse proportion if you’re doing Foundation Tier. If you’re doing Higher Tier then you also need to work through this lesson.