How to handle Vectors for GCSE Maths (Higher Tier)
In this post we’re going to look at how you deal with the more difficult kinds of questions you’ll encounter on the topic of Vectors for GCSE Maths at Higher Tier. If you haven’t already read through the post on the Vectors for GCSE Maths at Foundation Tier, I recommend that you take a look at that to make sure you understand the basics before you start on this one.
At Higher Tier, you’re expected to use your Foundation knowledge to solve problems and construct geometric arguments and proofs. With this type of question there’s usually no grid, so you can’t express the vectors in column vector form.
Example 1: A fairly simple proof
OAB (below) is a scalene triangle where 
= a and 
= b.
M and N are the midpoints of OA and OB, respectively.
Show that 
is parallel to 
.
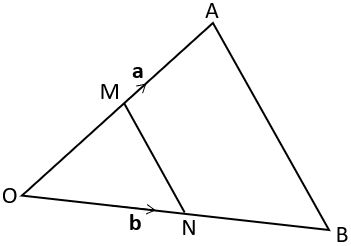
To show that two vectors are parallel, we need to show that one of them is a scalar multiple of the other. Since we don’t have a grid, we can’t do this with column vectors so we need to use expressions in terms of a and b only.
We know that the journey from A to B can be expressed as 
+
or –a + b
or b – a
So we hope that will turn out to be a multiple of (b – a).
Can you express in terms of a and b?
Answer: Since M is half way along ,
= 
a
And similarly, since N is half way along ,
= b
To get from M to N we go backwards along and forwards along ,
i.e. 
+
= – a + b
= (b – a)
So = 
;
is a scalar multiple of , so the two vectors are parallel.
[Remember, with a Show that” or “Prove that” question, you should ALWAYS end with a statement echoing the question!]
Your turn
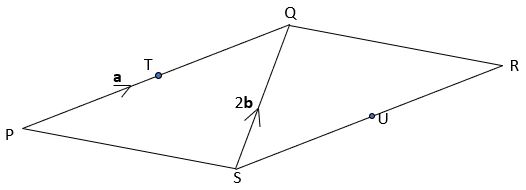
PQRS ia a parallelogram where 
= a and the diagonal 
= 2b.
T is the mid-point of PQ and U is the mid-point of SQ.
Prove that 
= 
.
Example 2: Solving a problem involving ratio
On the same triangle OAB that we used in Example 1, point P divides AB such that AP : PB = 3 : 1. Express the vector 
in terms of a and b.
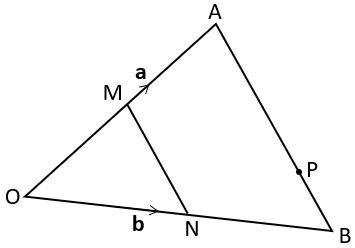
If the ratio AP : PB is 3 : 1 then P must be 
of the way from A to B.
So 
= 
and 
= 
.
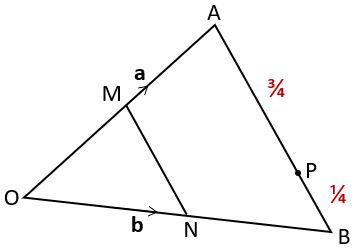
And of course we’ve already worked out that = b – a
If the ratio AP : PB is 3 : 1 then P must be of the way from A to B.
So = (b – a)
and = 
(b – a).
To get from O to P, we can choose to go via either A or B.
Via A: = +
= a + (b – a)
= a + b – a
= a + b
Via B: = + 
= b + – (b – a)
= b – b + a
= a + b
Your turn
The parallelogram used previously is shown below.
PS has been extended so that S is now the mid-point of PV.
Point W divides QR in the ratio 1 : 2.
Express vector 
in terms of a and b.
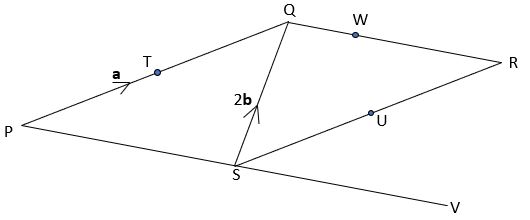
Check your answer here.
Example 3: Are these two vectors parallel?
Looking at triangle OAB again, use vectors to establish whether 
is parallel to .
First try it yourself: Express in terms of a and b. What can you conclude?
Solution:
We know that = a, and that a and b are not parallel to each other (otherwise we wouldn’t have a triangle!),
so for to be parallel to , it will need to be a multiple of a only, with no element of b.
From earlier, = (b – a)
and 
= b
so = +
= b – (b – a)
= b – b + a
= a + b
Since this includes an element of b, it is not a scalar multiple of and so cannot be parallel to .
You can also use this approach to show that three points (or two vectors) are on the same straight line:
If two vectors are parallel and have a point in common, then they must both be part of the same straight line.
Sample exam question
This question is taken from an AQA GCSE specimen paper.
In triangle ABC,
M is the mid-point of AC
N is the point on BC where BN : NC = 2 : 3
= 2a
= 3b
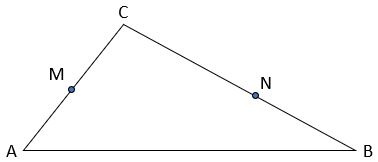
(a) Work out in terms of a and b, giving your answer in its simplest form.
(b) Use your answer to part (a) to explain why MN is not parallel to AB.
Check your answers here.
That covers the Higher content on Vectors for GCSE Maths; if you’ve managed to work through these examples and questions then you should be able to cope with any Vectors question that the exam board throws at you!
If you found it helpful then please share it with anyone else who you think would benefit (use the social sharing buttons if you like). If you have any suggestions for improvement or other topics that you’d like to see covered, then please comment below or drop me a line using my contact form.
On my other site at mathscourses.co.uk I have great-value courses covering the whole Foundation GCSE spec, and also a “Flying Start to A-level Maths” course that will help you to make sure you’re ready to start the A-level course, and will help you to achieve top grades in the GCSE at the same time.
If you’d like to be kept up to date with my new content then please sign up to my mailing list using the form at the bottom of this page, which will also give you access to my collection of free downloads.
Answers
Proof question
= + 
= a – 2b
= a
and, since the shape is a parallelogram, 
= = a
so 
= a
So = + +
= a – 2b + a
= a – 2b
So = = a – 2b.
Problem solving with ratio
We already know that = a – 2b
and so 
must also be a – 2b,
making 
equal to -(a – 2b), or 2b – a.
is also the same as , i.e. a – 2b again.
Since the ratio QW : WR is 1 : 2, W is 
of the way along QR
so 
= (a – 2b).
So vector = + +
= (2b – a) + 2b + (a – 2b)
= 2b + 2b – 
b – a + a
= 3 b – a
or 
b – a
Exam question
(a) To get from M to N we can choose from two routes:
(1) M to A to B to N
(2) M to C to N (perhaps a little easier)
Option (1):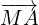 
+ + 
= – 
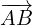= – (2a) = – a
In order to find an expression for 
, we need to find one for .
Since BC is split in the ratio BN : NC = 2 : 3, = 
so we need an expression for 
first:
To get from B to C it’s 
+ , which is -3b + 2a, or 2a – 3b
so = 
(2a – 3b) = 
a – 
b
and = +
= 3b + a – b
= a + 
b
So = +
= – a + a + b
= – 
a + b
or (9b – a).
Option (2):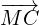 
+ 
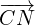
= = (2a) = a
= – 2a + 3b = 3b – 2a
= 
= 
(3b – 2a)
= b – a
= +
= a + b – a
= b – a
or (9b – a).
(b) is not a scalar multiple of (since = 3b and contains both as and bs, and there’s no single number that you can multiply 3b by to get something with both as and bs in it) so the two vectors cannot be parallel.
One Comment