Fractional indices: Essential skills for GCSE and A-level Maths
This article is Part 2 of a two-part series.
Part 1 covers all the Foundation content – basics, laws of indices, negative indices – and you can find it here.
In this post we’re picking up where that one left off, and moving on to look at fractional indices (needed for Higher GCSE spec and for A-level).
The image below shows an example of the kind of expression using fractional indices that you can expect to encounter and should be able to handle.
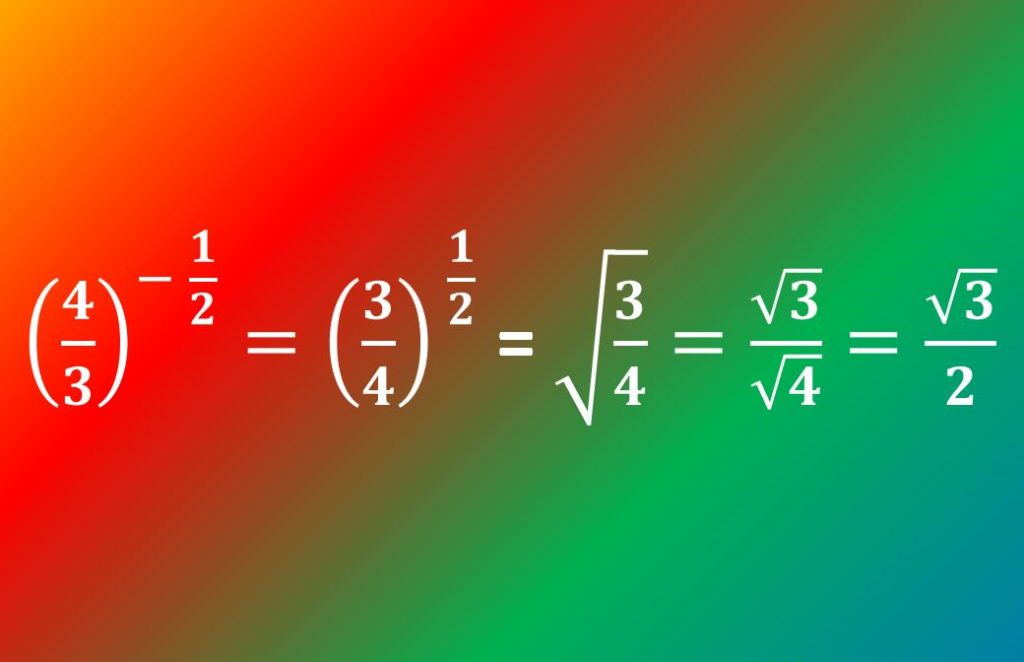
The laws of indices
We covered these in the previous lesson, but here’s a reminder:
- 1st law:

- 2nd law:
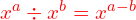
- 3rd law:
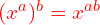
How do fractional indices work?
Take a look at the expressions below, which involve simple fractional indices, and apply the laws of indices to simplify them as far as possible:
In each case you should get the same answer: ![]() , which of course is simply
, which of course is simply ![]() .
.
What do you have to multiply by itself to get ![]() ? Compare your answer with example 1.
? Compare your answer with example 1.
What do you have to square to get ![]() ? Compare your answer with example 2.
? Compare your answer with example 2.
What do you have to do to get from ![]() to just
to just ![]() ? Compare your answer with example 3.
? Compare your answer with example 3.
In each case we need the square root…
… so ![]()
What if we’d started with ![]() ? How many of those would you need to multiply together to get
? How many of those would you need to multiply together to get ![]() ?
?
Answer: ![]()
… so ![]()
And more generally,
![]()
Note: As with surds, a fractional power indicates only the positive root; you only need to worry about the possibility of a second, negative, root if you’ve started off with the statement ![]() or
or ![]() , etc.
, etc.
Your turn: Work out the values of:
What if the numerator is greater than 1?
If the numerator is not simply 1 then we need to apply the 3rd law, but having the power in fractional form makes it look a little different from what we’ve encountered before:
![]()
Of course, ![]() is the same as
is the same as ![]() and
and ![]() ; both give the same result so it doesn’t matter whether you do the root first and then the integer power, or the integer power and then the root – though generally it’s easiest to take the root first.
; both give the same result so it doesn’t matter whether you do the root first and then the integer power, or the integer power and then the root – though generally it’s easiest to take the root first.
Now evaluate:
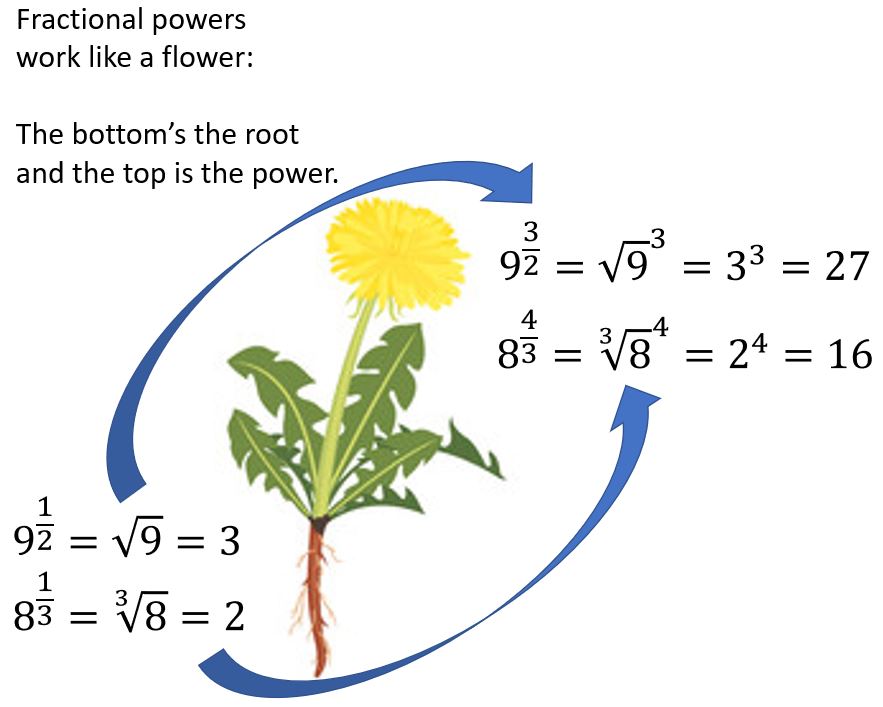
This “flower power” meme might help you to remember how to deal with fractional indices:
Adding in negative indices
Remember, any number to the power of ![]() is its own reciprocal. It doesn’t actually matter whether you do the reciprocal bit first or the fractional indices bit first, but I’d usually suggest getting rid of the negative powers as early as possible.
is its own reciprocal. It doesn’t actually matter whether you do the reciprocal bit first or the fractional indices bit first, but I’d usually suggest getting rid of the negative powers as early as possible.
Here’s an example:
![]()
Now here are some for you to have a go at:
And of course the example in the image at the beginning of this article should make sense to you now too!
Mixing it up with algebra
Now have a go at these questions involving a mixture of negative and fractional indices combined with algebraic expressions. Some of them are quite challenging – take care to double-check your working as it’s very easy to make mistakes!
- Express
 in index form.
in index form. - Expand and simplify
 , giving your answer in surd form (i.e. using surds rather than indices).
, giving your answer in surd form (i.e. using surds rather than indices). - Given that
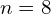 , evaluate
, evaluate 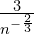
- Given that
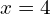 , evaluate
, evaluate 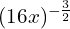 .
. - Express
![Rendered by QuickLaTeX.com 3\sqrt[3]{y} \times (8y)^\frac{4}{3}](https://b28mathstutor.co.uk/wp-content/ql-cache/quicklatex.com-5ea23ea4a16eab3d8a8c3e6174b1cac0_l3.png) in surd form.
in surd form. - Simplify
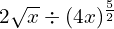 .
.
If you got all of those right then you’ve done exceptionally well!
Here’s a great codebreaker activity from JustMaths that I use with my Higher Tier and A-level students to practise negative and fractional indices (it downloads as a PDF).
And that covers fractional indices!
I hope you’ve found this post helpful. If you have then please share it, and also please take a look at the rest of my site to see what other help I can offer.
Answers
How do fractional indices work?
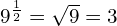
![Rendered by QuickLaTeX.com 64^\frac{1}{3} = \sqrt[3]{64} = 4](https://b28mathstutor.co.uk/wp-content/ql-cache/quicklatex.com-7c85878c37d06a877aa2a2451c9f49bf_l3.png)
![Rendered by QuickLaTeX.com 10000^\frac{1}{4} = \sqrt[4]{10000} = 10](https://b28mathstutor.co.uk/wp-content/ql-cache/quicklatex.com-54f3fd4310da7e3826e2e7ae03b34361_l3.png)
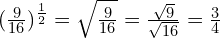
 (Yes, you will sometimes end up with surds!)
(Yes, you will sometimes end up with surds!)
Numerator greater than 1
Adding in negative indices
Mixing it up with algebra
1. ![]()
2. ![]()
![]()
![]()
3. ![]()
![]()
![]()
4. ![]()
![]()
![]()
5. ![]()
![]()
![]()
![]()
![]()
6. ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.

