Differentiation and stationary points
This article is part 2 of a series on differentiation; part 1 can be found here.
It will be relevant to you if you are studying any of:
- Edexcel IGCSE Maths
- A-level Maths
- BTEC Level 3 Engineering (Module 7)
… or any other course that involves Calculus.
In part 1 we introduced the idea of differentiation and covered how to use it with simple algebraic functions and their gradients. In this instalment we’re focusing on finding, and identifying the nature of, stationary points.
Stationary points
Types of stationary point
A stationary point is any point on a curve where the gradient of the graph is zero.
A stationary point can be a maximum point, a minimum point or a point of inflection. In this article we’re focusing on maximum and minimum points. Collectively, these are also known as turning points, since they are where the gradient changes from positive to negative or vice versa.
(A point of inflection is a point where the tangent to the curve crosses the curve. The gradient may or may not be zero at that point; if it is then we have a stationary point of inflection, but not a turning point.)
How to find a stationary point
To find a stationary point using calculus, we differentiate the equation of the curve and make ![]() equal to zero, then solve to find which value(s) of
equal to zero, then solve to find which value(s) of ![]() give a gradient of zero.
give a gradient of zero.
For example, to find the stationary point on the quadratic curve ![]() using differentiation:
using differentiation:
First, differentiate: ![]()
Then put ![]() equal to zero and solve:
equal to zero and solve:![]()
![]()
![]()
Now that we have the x-coordinate of the stationary point, we can substitute that back into the equation of the original curve to find the y-coordinate:![]()
So the coordinates of the stationary point are ![]()
(Of course, with a quadratic curve you can also find the x-coordinate of the turning point by other means – completing the square or taking the mean of the x-intercepts – but these methods can’t be used with other types of function. Differentiation is far more versatile!)
Your turn 1
For each of the functions listed below, find the first derivative ![]() , and hence find the coordinates of any stationary points.
, and hence find the coordinates of any stationary points.
Identifying the nature – maximum or minimum?
For Level 2 courses such as the AQA Level 2 Certificate in Further Maths, you only need to be able to identify maximum and minimum points in cases where you are familiar with the graph shape and so can identify them that way. The key points at this level are:
- A quadratic curve will have a minimum point (“happy face curve”) if the coefficient of the
 is positive, and a maximum point (“sad face curve”) if it’s negative.
is positive, and a maximum point (“sad face curve”) if it’s negative. - A cubic curve with a positive
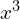 term will have a general upward trend from left to right and will usually follow an N shape. If the
term will have a general upward trend from left to right and will usually follow an N shape. If the  term has a negative coefficient then the shape will be mirrored, going from top left to bottom right.
term has a negative coefficient then the shape will be mirrored, going from top left to bottom right.
However, for Level 3 courses you’re expected to be able to determine the nature of a stationary point without necessarily knowing the shape of the curve.
Evaluating points on either side
How can we decide whether an identified stationary point is a maximum or a minimum? Well, one way is to look at the y-coordinates of points just on either side of the stationary point.
For example, the curve ![]() has a stationary point at
has a stationary point at ![]() . Calculate the y-coordinates when x = 0 and when x = 2. In this example, when x is 0, y = 5 and and when x = 2, y is also 5 (as you’d expect with the symmetry of a quadratic curve). Since both of these points are higher than
. Calculate the y-coordinates when x = 0 and when x = 2. In this example, when x is 0, y = 5 and and when x = 2, y is also 5 (as you’d expect with the symmetry of a quadratic curve). Since both of these points are higher than ![]() , we know that our stationary point must be a minimum.
, we know that our stationary point must be a minimum.
With some types of curve it’s important to choose points close to the identified stationary point, since a point further away might be on a different section of the curve and give a misleading impression.
A maximum isn’t always the highest point!
You might think that, where a curve has two stationary points, the y-coordinate of each point will tell us which is a maximum and which is a minimum. That’s true for a cubic curve, where a maximum point will always have a higher y-coordinate than a minimum, but it can’t be relied on for a curve that isn’t continuous. For example, the graph of ![]() looks like this (below). As you can see, the minimum point at
looks like this (below). As you can see, the minimum point at ![]() is actually higher than the maximum point at
is actually higher than the maximum point at ![]() .
.
And if you were to try substituting x = 0 into the equation of the curve then you’d run into problems because there’s an asymptote there!

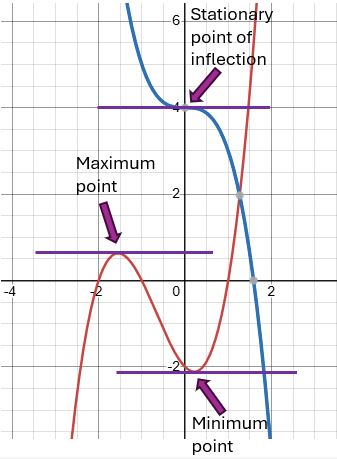
It should also be noted that, even on a continuous curve, a maximum/minimum point isn’t necessarily the highest/lowest point on the whole curve. For example the image below shows a typical cubic curve; the section to the right goes much higher than the maximum point where x = 1, and the section to the left goes much lower than the minimum point where x = 3.

In a case like this, it’s more accurate to refer to a stationary point as a “local maximum” or a “local minimum” – i.e. it’s only the highest/lowest point on a particular section of the curve. But in practice we often omit the “local” bit.
Using differentiation to identify the nature of a stationary point
Remember how we said that ![]() was called the “first derivative”? This suggests that there’s also a second derivative (and maybe even third, fourth and fifth derivatives).
was called the “first derivative”? This suggests that there’s also a second derivative (and maybe even third, fourth and fifth derivatives).
Indeed there is, and we can use the second derivative to decide whether a stationary point is a maximum or a minimum. In fact this is the method most commonly used.
The second derivative
When we differentiate y with respect to x, we get ![]() , or the gradient of the curve, also described as the rate of change of y.
, or the gradient of the curve, also described as the rate of change of y.
When we differentiate for the second time, we’re differentiating ![]() to get
to get ![]() , or the rate of change of the gradient. This is usually written as
, or the rate of change of the gradient. This is usually written as ![]() and pronounced “d 2 y by d x squared”.
and pronounced “d 2 y by d x squared”.
Now let’s think about what “rate of change of gradient” actually means.
If the rate of change of the gradient is positive then that means that the gradient is increasing. It doesn’t necessarily mean that it’s getting steeper though; it might be going from 1 to 4 to 10, in which case it is getting steeper, but on the other hand it might be changing from -10 to -4 to -1, moving upwards towards zero. Both indicate an increase in the gradient.
The image below shows a curve with increasing gradient. On the left, where x is -3, we have a steep negative gradient. As we move to the right, the gradient increases towards zero, becoming less and less steep until it reaches zero at the stationary point and then becomes positive and continues to increase.
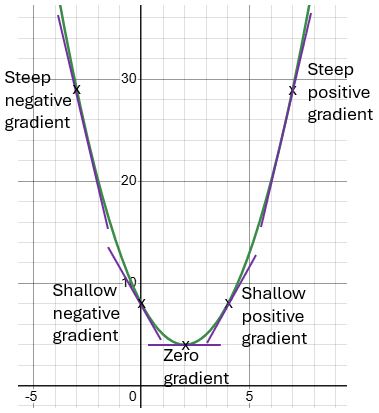
So if the gradient is increasing as the curve passes through a stationary point then that means it’s going from negative to positive and so the stationary point must be a minimum.
Hence a positive second derivative at a stationary point means that the stationary point is a minimum.
Conversely, if the second derivative is negative at a stationary point then that means that the gradient is decreasing. Since the curve is going through a stationary point where the gradient is zero, it must be going from a positive gradient to a negative one and so the stationary point must be a maximum.
So in summary,
- If the second derivative at a stationary point is positive then the point is a minimum.
- If the second derivative at a stationary point is negative then the point is a maximum.
If the second derivative is exactly zero then you might think that the stationary point must be a point of inflection. Unfortunately it’s not that simple; it might be a point of inflection but it might be a maximum or minimum point, so you also need to use the method of checking points on either side to be sure. But you don’t need to worry about that until the second year of the A-level course.
Example
If ![]() then
then ![]()
So we have stationary points when ![]()
![]()
Either x = 0 or x = -2
When x = 0, y = 0 so there is a stationary point at (0, 0)
When x = -2, y = (-2)³ + 3(-2)² = 4, so there is a stationary point at (-2, 4)
(We can omit this step if only the x-coordinate is required.)
Differentiating again, ![]()
When x = 0, ![]() ; 6 > 0 so the stationary point is a minimum.
; 6 > 0 so the stationary point is a minimum.
When x = -2, ![]() ; -6 < 0 so the stationary point is a maximum.
; -6 < 0 so the stationary point is a maximum.
You can shorten the last section a little by writing it in this form:![]()
… BUT make sure you include the bit about it being positive or negative and what that means!
Your turn 2
Here again are the curves from the previous exercise. Use differentiation to find the nature of the stationary point(s) in each case.
You might also like to try to sketch the shape of each graph – this should be straightforward for 1 and 2, but less so for 3 and 4 – and then use Desmos to plot the graphs accurately and see if they look as you predicted.
Still to cover…
As mentioned in part 1, differentiation can also be used to identify intervals of increase and decrease (i.e. for which values of x the value of y is going up or down / the gradient is positive or negative.)
It can be used in the context of kinematics to move between displacement, velocity and acceleration.
And it can be used to solve optimisation problems in practical situations.
I’ll cover these in future posts.
If you’ve found this article helpful then please share it with anyone else who you think would benefit (use the social sharing buttons if you like). If you have any suggestions for improvement or other topics that you’d like to see covered, then please comment below or drop me a line using my contact form.
On my sister site at at mathscourses.co.uk you can find – among other things – a great-value suite of courses covering the entire GCSE (and Edexcel IGCSE) Foundation content, and the “Flying Start to A-level Maths” course for those who want to get top grades at GCSE and hit the ground running at A-level – please take a look!
If you’d like to be kept up to date with my new content then please sign up to my mailing list using the form at the bottom of this page, which will also give you access to my collection of free downloads.
Answers:
Your turn 1 answers
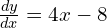 ; SP at
; SP at 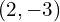
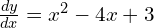 ; SPs at
; SPs at 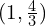 and
and 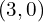
 ; SP at
; SP at 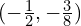
 ; SP at
; SP at 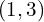
Click here to return to questions
Your turn 2 answers
- (a)
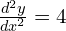 ; 4 > 0 so stationary point is a minimum
; 4 > 0 so stationary point is a minimum - (a)
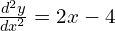
When x = 1,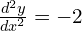 ; -2 < 0 so stationary point is a maximum
; -2 < 0 so stationary point is a maximum
When x = 3,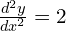 ; 2 > 0 so stationary point is a minimum
; 2 > 0 so stationary point is a minimum - (a)
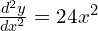
When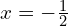 ,
, 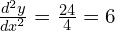 ; 6 > 0 so stationary point is a minimum
; 6 > 0 so stationary point is a minimum - (a)
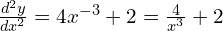
When x = 1,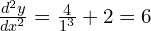 ; 6 > 0 so stationary point is a minimum
; 6 > 0 so stationary point is a minimum

