Confused by BIDMAS / BODMAS / BEDMAS / PEMDAS? Try GEMA!
Remind me again, what’s BIDMAS?
If you grew up in the UK then it’s likely that you’ve been taught BIDMAS or BODMAS to help you remember the order of operations – what order you should do things in – in Maths. In other parts of the world, it’s BEDMAS or PEMDAS.
(In PEMDAS, P = Parentheses and E = Exponent.)
But BIDMAS and all the rest can be misleading, and it’s easy to get confused. The main reasons for confusion are:
- Some forms of notation count as “invisible brackets”
- e.g. in
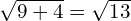, the roof of the root sign forms “invisible brackets”
- e.g. in
- Division and multiplication have equal priority
- (They are flip sides of the same coin: dividing by 3 is the same as multiplying by
, and vice versa)
- (They are flip sides of the same coin: dividing by 3 is the same as multiplying by
- Addition and subtraction have equal priority
- (They are flip sides of the same coin: subtracting 2 is the same as adding –2, and vice versa)
When multiplying and dividing, or when adding and subtracting, we normally work from left to right; you DON’T do all the multiplying before the dividing, or all the addition before the subtraction, unless it’s written in that order.
So what’s GEMA then?
An alternative acronym that you might find less confusing is GEMA:
First you work out any expressions that are grouped, for example:
- in brackets:
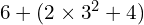
- under a root sign:
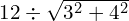
- in the numerator or denominator of a fraction:
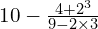– in this case 
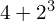is one grouping and 
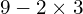is another.
Of course you will need to use the later steps within these groupings! Read on for some examples.
Exponent is another word for an index or power – which includes roots (since a root can be written as a power), e.g.
- with
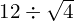you work out the 
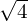first - with
you work out the 
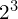first - with
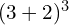you work out the 3 + 2 (the grouping) first and then cube it
With multiplication and division you just need to remember that the operator (x or ÷) belongs with the number immediately AFTER it. Generally it makes sense to work from left to right, but as long as you keep the operator with its number, the order doesn’t actually matter.
The same applies with addition and subtraction.
For example if you have 7 – 5 + 6 – 2 then you could do 7 take away 5, then add 6, then take away 2 (giving an answer of 6)…
OR
You could say, “We have positive 7 and positive 6, giving positive 13, and negative 5 and negative 2, giving negative 7, so overall we have +13 – 7 = 6.”
What you MUST NOT do – although BIDMAS might make you want to – is to say “Addition first, so we do 5 + 6 = 11, so that gives us 7 – 11 – 4, which is negative 8.”
Give it a try!
Now have a go at these, using GEMA, and then watch the video to see if you got them right. Don’t just go straight to the video, try it yourself first!
For more on how I can help you with your Maths, please visit this page.
If you’ve found this article helpful then please share it with anyone else who you think would benefit (use the social sharing buttons if you like). If you have any suggestions for improvement or other topics that you’d like to see covered, then please comment below or drop me a line using my contact form.
On my sister site at at mathscourses.co.uk you can find – among other things – a great-value suite of courses covering the entire GCSE (and Edexcel IGCSE) Foundation content, and the “Flying Start to A-level Maths” course for those who want to get top grades at GCSE and hit the ground running at A-level – please take a look!
If you’d like to be kept up to date with my new content then please sign up to my mailing list using the form at the bottom of this page, which will also give you access to my collection of free downloads.
Note for anyone struggling with LaTeX in WordPress
If you’re having difficulty getting LaTeX to display mathematical notation inline in WordPress as I did, try going into your theme customiser, looking for the “Additional CSS” option, and pasting in
.ql-img-inline-formula { display: inline;}
The plugin that I’m using to enable LaTeX is WP QuickLatex and I suspect that the code above is specific to this particular plugin, but you might be able to identify the equivalent code for whatever plugin you’re using.
