Working with surds
For Higher GCSE and beyond, you need to be able to work with surds.
This is Part 1 of a two-part series. Part 2 – on rationalising the denominator – can be found here, but make sure you’re comfortable with the content of Part 1 first.
Surds basics
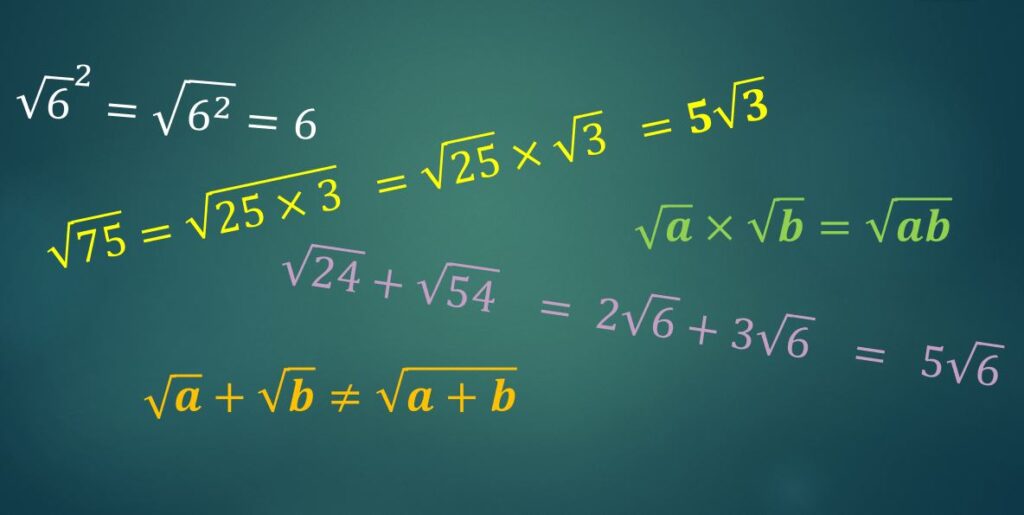
What is a surd?
A surd is the (positive) square root of a number that isn’t a square number.
For example, ![]() and
and ![]() are surds, because neither 3 nor 24 is a square number…
are surds, because neither 3 nor 24 is a square number…
… but ![]() isn’t a surd because 9 is a square number and so
isn’t a surd because 9 is a square number and so ![]() can be simplified to just 3.
can be simplified to just 3.
A surd is also an irrational number, which means it can’t be written as the ratio of two integers – or as a fraction, which is just a ratio written in a slightly different form.
Squaring and square rooting are inverse operations, i.e. they cancel each other out.
Using a square number to illustrate:![]() and similarly,
and similarly, ![]()
– it doesn’t matter whether you square first or take the square root first; you get the same result either way.
This works with surds too: ![]()
Combining surds
You can multiply and divide surds:
(Again, we’re using square numbers to illustrate the principle, but it works with non-square numbers too)
![]()
and![]()
so![]()
Or, more generally, ![]()
and similarly, ![]()
BUT you can’t add/subtract the number under the root sign:
![]()
but![]() which clearly is NOT the same as 5.
which clearly is NOT the same as 5.
So ![]()
and similarly
![]()
If you need to multiply or divide a mixture of surds and rational numbers, deal with each type of number separately, e.g.![]()
Your turn 1
Simplify where possible:
Manipulating surds
Simplifying a surd
This means making the number under the square root sign as small as possible. We do this by taking out a square factor – the biggest one we can.
Examples:![]()
![]()
Just as with cancelling down fractions, it doesn’t matter if you don’t immediately spot the biggest square factor. For example, with ![]() you might initially only spot that 4 is a factor, giving
you might initially only spot that 4 is a factor, giving![]()
but 20 also has a factor of 4 so we can take it further:![]()
If you’d spotted straight away that 16 was a factor then it would have got you to the same result more quickly:![]()
Adding and subtracting with surds
You can add and subtract quantities of the same surds – think of it as adding like terms in algebra.
For example, ![]() can be calculated if we can express both values as multiples of the same surd.
can be calculated if we can express both values as multiples of the same surd.
We already know that ![]()
and the square number 9 is a factor of 54 so we can say![]()
Now we have both values as multiples of ![]()
so![]()
Expanding brackets with surds
This works just as it does with algebra.
Examples:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
What happens when you expand ![]() ? Try it, then scroll down to see if you got it right.
? Try it, then scroll down to see if you got it right.
Solution:![]()
![]()
![]()
![]()
Notice how the surds cancel out so that you’re left with only rational numbers.
In fact it’s a case of “difference of two squares”, where ![]() .
.
(You’ll have encountered this before with quadratic expressions such as ![]() .)
.)
In this particular example ![]() and
and ![]() so we end up with
so we end up with ![]()
What would you need to multiply ![]() by to get an answer without any surds in it? Try it and see if you were right.
by to get an answer without any surds in it? Try it and see if you were right.
(If you do it right then you should end up with an answer of ![]() .)
.)
This pattern will come in handy when we look at rationalising the denominator, which I’ll cover in my next blog post.
Your turn 2
Part A: Simplify:
Part B: Expand and simplify as far as possible:
Now that you can manipulate surds, in the next post we’ll look at using these techniques to rationalise the denominator of a fraction.
Your turn 1 answers:
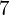
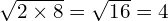

- Cannot simplify
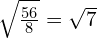
- Cannot simplify
Click here to return to questions
Your turn 2 answers:
Part A
Part B
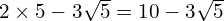
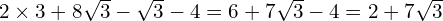
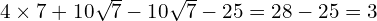
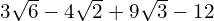 (won’t simplify any further)
(won’t simplify any further)

