This tutorial follows on from Part 1, which covered the skills you need to deal with simultaneous equation questions at GCSE Foundation level, using the elimination method – where you write the equations one above the other so that the like terms match up in columns.

Now we’re going to cover the substitution method, which is needed for Higher GCSE and for A-level.

What is the substitution method for solving simultaneous equations?

Why do we need another method?

In the scenarios we’ve looked at so far, both equations were usually given in the same format – usually ax + by = c – or could be rearranged into that format, so the like terms could be lined up.

But sometimes you might have to solve a pair of simultaneous equations where that’s not true. For example, you might need to solve these two equations simultaneously:
x² – y² = 8x
y = x – 3

As you can see, there’s no way that we can rearrange these two simultaneous equations to line up the like terms!

And in fact you can also use the substitution method in any situation where the elimination method would work (though, depending on the numbers involved, it may sometimes turn out to be a messier option!).

How it works

Essentially, we make one of the unknowns the subject of one of the equations, then substitute into the other equation so that that unknown is eliminated.

Example 1

Here’s an example using one of the simultaneous equation pairs from the first tutorial:

x + y = 10 and 3x – y = 22

This time, rather than lining the equations up with one above the other, we’re going to make y the subject of the first equation:
y = 10 – x

… and then substitute the 10 – x into the second equation to replace the y:
3x – (10 – x) = 22
[Note the use of brackets – essential since we are subtracting the whole expression for y.]

So now we have an equation that has only one unknown and so we can solve it, starting by expanding the brackets:
3x – 10 + x = 22
4x = 22 + 10 = 32
x = 32 ÷ 4
x = 8

Then it’s easy to substitute the value for x back into the rearranged first equation to get y:
y = 10 – x = 10 – 8
y = 2

Don’t forget to substitute both values back into the other equation to check that you’ve got it right!
3x – y = 3(8) – 2 = 22 ✔️

In the above example you could equally have made x the subject of the first equation (giving x = 10 – y) and made the substitution into the second to get an equation in y alone – try it and check that you get the same solution.

Example 2

3x + 4y = 14 and 2y = 4x + 18

The easiest thing to make the subject here is going to be the y in the second equation:
y = 2x + 9

Now substitute into the first equation to eliminate the y:
3x + 4(2x + 9) = 14

and solve for x:
3x + 8x + 36 = 14
11x = 14 – 36 = -22
x = -2

Then y = 2x + 9 = 2(-2) + 9 = -4 + 9
y = 5

Example 3

Now let’s look at the example mentioned earlier, where you have to use the substitution method:

x² – y² = 8x and y = x – 3

In this case y is already the subject of one equation so we might as well use that (though you could make x the subject and use that instead – try it afterwards!).
Substitute x – 3 into the first equation in place of y and you get
x² – (x – 3)² = 8x

Expanding the brackets gives us
x² – (x² – 6x + 9) = 8x
x² – x² + 6x – 9 = 8x
The two x²s cancel out to give
6x – 9 = 8x
-9 = 2x
-4.5 = x

And substituting back into the second equation we get
y = x – 3 = -4.5 – 3
y = -7.5

You’ll want a calculator to check this one but it’s worth doing if you can!
LHS: x² – y² = (-4.5)² – (-7.5)² = -36
RHS: 8x = 8(-4.5) = -36
LHS = RHS ✔️

Your turn 1

Now you try it with these pairs of simultaneous equations. In question 2 you’re finding a and b rather than x and y, but it works in exactly the same way.

3x – 2y = 11 and 5x – 4y = 19 (Start by making y the subject of the first equation)
4a + 5b = 17 and 6a = 2b – 3 (I suggest making b the subject here)
3xy + x – 2y = 22 and y = 2x + 1 (2 sets of solutions for this pair!)

Click here for the solutions

Simultaneous equations and graphs

When you solve a pair of simultaneous equations, you’re also finding the point(s) of intersection of the two graphs described by the equations.

Using the straight lines given by the two equations we started with in Example 1 above, the red line on the image below is x + y = 10 and the blue one is 3x – y = 22. The point where they intersect has the coordinates (8, 2), matching the x-and y-values found by solving the equations simultaneously – because that is the only point at which both equations are true, i.e. it’s the only point that’s on both lines.

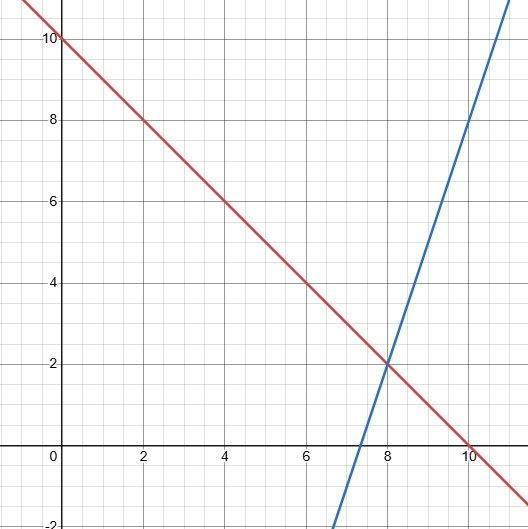
Solving a pair of simultaneous equations - by elimination or by substitution - finds the point(s) of intersection of two graphs.

(If you want to know more about how straight line graphs work then I have a series of tutorials that you can find here.)

This is also true with other types of graph, where there might be more than one point of intersection; see later for an example.

Harder questions involving quadratics

The equations in the last example above were carefully chosen so that the x² terms conveniently cancelled out and we didn’t have to solve a tricky quadratic equation, because as you read this I don’t know whether solving three-term quadratics (ax² + bx + c = 0) is a skill that you’ve already covered. I’m afraid it won’t always be that easy though – sometimes you will end up with a quadratic to solve.

If you haven’t already covered quadratics then you’ll probably want to stop here, but if you have and are aiming for a high grade then stay with me and we’ll look at some harder questions.

Example

x² + y² = 25 and 2y =x + 10

Make x the subject of the second equation (you could use y instead, but that would mean working with fractions, which could get messy):
2y – 10 = x

Substitute into the first equation:
(2y – 10)² + y² = 25

Expand brackets and collect like terms:
4y² – 40y + 100 + y² = 25
5y² – 40y + 75 = 0
Divide through by 5:
y² – 8y + 15 = 0

Factorise and solve:
(y – 3)(y – 5) = 0
So y = 3 or y = 5

Substitute back into the rearranged second equation to find the corresponding x-value for each y-value:
When y = 3, x = 2(3) – 10 = -4
When y = 5, x = 2(5) – 10 = 0

So the solutions are x = -4, y = 3 and x = 0, y = 5.

Notice how in this case we have two solutions. This will happen if the equations we start with are of a line and a curve – or two curves – and they intersect in two places.
In this particular example we have a circle (x² + y² = 25) and a line (2y = x + 10) which intersect at (0, 5) and (-4, 3); these are the only points where the equation of the circle and the equation of the line are both true, so they match the solutions to the simultaneous equations.

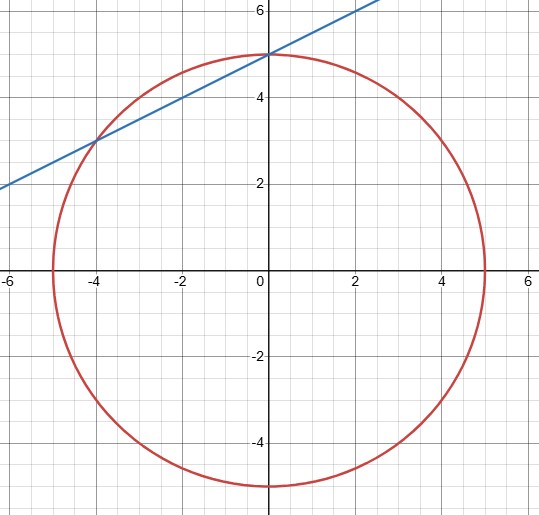
Your turn 2

Here are some harder simultaneous equations for you to solve. When you’ve worked them out, you might want to try putting the equations into Desmos so you can see how the graphs intersect.

xy = 2 and y = x + 1
xy – 2y – x = 2 and x + y = 7
y² – x² = 60 and y = 3x + 2

Click here for the answers

Simultaneous equations with more than two unknowns

It’s also possible to have three unknowns, in which case three equations are required in order to solve them. (Or even four unknowns and four equations, though you’re very unlikely to have to deal with that scenario!) In such a case you take the same approach, eliminating one variable at a time until you get it down to a single solvable equation with a single unknown.

If you do encounter a question with three unknowns then you’ll usually find that at least one of the equations contains only two unknowns so you can use that one to eliminate the third unknown in the other two equations. For example, equations 1 and 2 might contain xs, ys and zs but equation 3 might have only xs and zs. Make z the subject of equation 3 and substitute into the other two equations, and you’re left with two equations in just x and y (or, if it’s easier, make x the subject and get two equations in y and z)… and you already know how to deal with those.

So that covers everything you need to know about solving simultaneous equations, for GCSE and for A-level.

If you’ve found this article helpful then please share it with anyone else who you think would benefit (use the social sharing buttons if you like). If you have any suggestions for improvement or other topics that you’d like to see covered, then please comment below or drop me a line using my contact form.

On my sister site at at mathscourses.co.uk you can find – among other things – a great-value suite of courses covering the entire GCSE (and Edexcel IGCSE) Foundation content, and the “Flying Start to A-level Maths” course for those who want to get top grades at GCSE and hit the ground running at A-level – please take a look!

If you’d like to be kept up to date with my new content then please sign up to my mailing list using the form at the bottom of this page, which will also give you access to my collection of free downloads.

Answers

Your turn 1 answers:

x = 3, y = -1
a = ½, b = 3
x = 2, y = 5 and x = -2, y = 3 (remember, if x² = 4 then x has two possible values!)

Click here to return to questions