How to round numbers for GCSE Maths

For both Foundation and Higher GCSE – and also for other Level 2 Maths qualifications – you need to know how to round numbers:

• to the nearest whole number, ten, hundred or thousand
• to the nearest tenth or hundredth
• to a specified number of decimal places
• to a specified number of significant figures.

How to round numbers by place value

The first two categories could also be described as rounding by place value .

How to round numbers to the nearest whole number (integer)

Rounding to the nearest whole number means rounding to the units column. On the image above, the units digit is the 5. So the number is 12,345-and-a-bit.

Now we need to decide whether the number we have is closer to 12,345 or 12,346. To do that, look at the digit AFTER the one you’re interested in. If that next digit is 5 or more then that tells us that we’re at least half way to the next whole number, so we should round UP.

In this case the next digit is a 6, which tells us that the number is more than 12,345 and a half, so we need to round the 5 up to a 6, giving 12,346 to the nearest whole number.

How to round numbers to the nearest ten

To round to the nearest ten, identify which is the tens digit.
On the image above, it would be the 4.

Now we need to decide whether the number we have is closer to 12,340 or 12,350. Again, look at the next digit AFTER the one you’re interested in. If that next digit is 5 or more then that tells us that we’re at least half way to the next tens digit.

In this case the next digit is a 5 so we know that the number is actually at least 12,345, which means it’s closer to 12,350 than to 12,340. So we round the 4 up to a 5, and pad out the remaining space to the decimal point with a zero, so that all the digits are still in the right place value columns (giving 12350 rather than 1235, which is a much smaller number).

How to round numbers to the nearest hundred

The number in the hundreds column is the 3, so the question is, is our number closer to 12,300 or 12,400?

Look at the next digit: it’s a 4, so the number must be twelve thousand, three hundred and forty-something; in order words, it’s definitely less than 12,350, so it’s closer to 12,300 than to 12,400.
So in this case we DON’T round the 3 up, but just leave it as a 3. Again, we need to pad out the gap to the decimal point with zeroes, to keep the digits in the right columns… so we get 12,300 rather than the much smaller 123.

How to round numbers to the nearest tenth

Now try rounding the same number to the nearest tenth. Can you predict what the answer will be?
The tenths column is the first one after the decimal point, so it’s the 6.
The digit immediately after it is a 7, so we’re more than half way up from 12,345.6 to 12,345.7, so the 6 needs to rounded up, and the rounded value is 12,345.7.

(No need to pad out with zeroes in this case, because we can already see where the decimal point is.)

Rounding to a specified number of decimal places (d.p.)

Once you’ve got your head around rounding to the nearest tenth, hundredth or thousandth, this is easy.
Rounding to 1 decimal place is the same as rounding to the nearest tenth;
rounding to 2 decimal places is the same as rounding to the nearest hundredth;
rounding to 3 decimal places is the same as rounding to the nearest thousandth;
and so on.

So what would 34.527 be if you rounded it (a) to 1 d.p.? (b) to 2 d.p.?

Answers: (a) 34.5; (b) 34.53

Rounding to a specified number of significant figures (s.f.)

This is a little harder to get to grips with. The tricky bit is identifying which digit you’re interested in. Once you’ve done that, it’s just the same as the other approaches.

The first significant figure is the first digit that isn’t a zero. After that, EVERY digit is a significant figure, including zeroes.

So in 3805, the first significant figure is the 3, the second is the 8 and the third is the 0.
What would this number be to 1, 2 and 3 s.f.?

1 significant figure: First s.f. is the 3. Next digit after the 3 is 8, which is “5 or more”, so we round the 3 up to a 4 and pad out with zeroes so that it stays in the thousands column, giving 4000.
2 significant figures: Second s.f. is the 8. Next digit after the 8 is a 0, which is NOT “5 or more”, so we leave the 8 as an 8 and pad out with zeroes, giving 3800.
3 significant figures: Third s.f. is the 0. Next digit after the 0 is a 5, which is “5 or more” so we round the 0 up to a 1, and pad out with zeroes, giving 3810.

Now can you round 0.04097 to 1, 2 and 3 s.f.?

1 s.f.: First s.f. is the 4. Next digit after the 4 is 0, which is NOT “5 or more”, so we leave the 4 as it is, giving 0.04.
2 s.f.: Second s.f. is the 0. Next digit after the 0 is a 9, which is “5 or more”, so we round the 0 up to a 1, giving 0.041.
3 s.f.: Third s.f. is the 9. Next digit after the 9 is a 7, which is “5 or more” so we round the 9 up to a 10… which means that the 1 has to be added onto the next column to the left, giving 0.410.

When dealing with decimal places, DO NOT add any extra zeroes at the end, or it makes it sound as if you’re being more accurate than you actually are. Remember, extra zeroes are only needed to show the positions of the digits in relation to the decimal point.

Video lesson

This video lesson, showing you how to round numbers, is an extract from my Grade 4 Essentials for GCSE Maths course (Number & Ratio module). You can read more about the course on this page, and find the course itself at mathscourses.co.uk.

Practice grid

Now that you know how to round numbers, you can use this table for more practice. It’s entirely up to you whether you use all the columns; if you’re confident going straight to the answer column without filling the others in then that’s great.
Answers below.

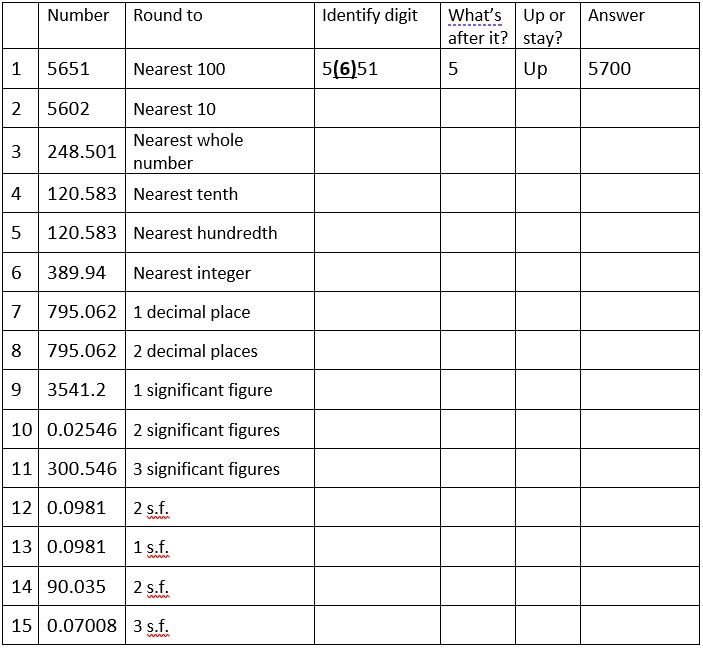
Answers: 2) 5600; 3) 249; 4) 120.6; 5) 120.58; 6) 390; 7) 795.1; 8) 795.06; 9) 4000; 10) 0.03; 11) 301; 12) 0.098; 13) 0.10 (since the 2nd s.f. in the original number was the hundredths digit so we’re rounding to the nearest hundredth); 14) 90; 15) 0.0701

Now that you’ve got rounding sussed, the next stage in this topic is working with upper and lower bounds, which I cover in this blog post.

Have you found this post helpful? If so, please let me know by commenting below, and share it with anyone else you know who might find it helpful.

What other Maths topics would you like to see me cover in my blog posts? Comment below and let me know.