How to do calculations with Standard Form for GCSE Maths
In last month’s blog post we covered the basics of standard form: what it is and how to convert numbers into and out of it, including numbers that are in almost-but-not-quite standard form, such as 26 × 10³ or 0.74 × 10⁵.
This tutorial follows on from that, and shows you how to do calculations with numbers given to you in standard form. The first two sections – multiplication, division, addition and subtraction – are the top end of the Foundation content for GCSE, and the rest is Higher only.
Of course, in questions where a calculator is allowed you won’t need to use most of these skills; you just need to know how to enter the numbers into your calculator using the standard form button. (Exceptions are questions with very large powers of 10 and the algebraic questions covered in the later sections, where a calculator won’t be of much help.) But most of what you’ll find here is the kind of question you’ll get on a non-calculator paper.
Multiplying and dividing numbers in standard form
This is pretty straightforward: simply multiply/divide the first parts and the powers of 10 separately.
Multiplication example
(4 × 10⁷) × (3 × 10³)
We can ignore the brackets since everything is multiplied.
= 4 × 3 × 10⁷ × 10³
Use the 1st law of indices, ![]()
= 12 × ![]()
=12 × 10¹⁰
If the first part of the result is a number between 1 and 10 then you’re done, but as you can see that’s not the case here. So this is where the not-quite-standard form conversion comes in.
To turn the 12 into a number between 1 and 10 we need to divide by 10 to give 1.2,
which means we need to balance that by multiplying the other bit by 10, i.e. increasing the power of 10 by one
so we end up with an answer, in standard form, of
1.2 × 10¹¹
Division example
(6 × 10⁴) ÷ (8 × 10⁷)
= 6 ÷ 8 × 10⁴ ÷ 10⁷
or ![]()
2nd law of indices: Dividing means subtracting the indices
= 0.75 x ![]()
= 0.75 × 10⁻³
Again, this is not-quite-standard form; we need to multiply the 0.75 by 10 to get 7.5,
and divide the 10⁻³ by 10 to get 10⁻⁴ (remember, going down 1 from -3 ont he number line takes you to -4)
so the answer in standard form is
7.5 × 10⁻⁴
Your turn 1
Without using a calculator, find the answers to these calculations in standard form.
- (3 × 10⁴) × (2 × 10³)
- (4 × 10⁴)²
- (4 × 10⁵) × (6 × 10⁻⁷)
- (8.4 × 10⁷) ÷ (2 × 10³)
- (6 × 10⁻⁷) ÷ (5 × 10⁴)
- (3 × 10⁷) ÷ (5 × 10⁻³)
Adding and subtracting numbers in standard form
This is a bit like adding or subtracting fractions:
To be able to add/subtract fractions, you have to put them both over the same denominator – in other words, into the same units.
To add/subtract numbers in standard form, we have to put THEM into the same units too; in this context that means they both need to be in terms of the same power of 10.
Example
(4 × 10⁴) + (3 × 10³)
We need to start by getting both numbers into the same power of 10; it’s usually best to put them both into the highest power, i.e. 10⁴.
[You can use the lower power if you like but then you’re more likely to need to do another conversion at the end of the process, especially with addition.]
10³ x 10 = 10⁴ so we balance that by dividing the 3 by 10 to get 0.3:
3 × 10³ = 0.3 × 10⁴
Now we can simply add the 4 and the 0.3:
4 × 10⁴ + 0.3 × 10⁴ = (4 + 0.3) × 10⁴
= 4.3 × 10⁴
As before, if the answer is in not-quite-standard from then you need to convert it back to standard form – for example
(1.2 × 10⁴) – (7 × 10³)
[Of course the brackets aren’t really necessary since multiplication takes priority over addition anyway]
= 1.2 × 10⁴ – 0.7 × 10⁴
= 0.5 × 10⁴
= 5 × 10³
Your turn 2
Without using a calculator, find the answers to these calculations in standard form.
- (3.5 × 10⁴) + (2.1 × 10³)
- (3.1 × 10⁻⁴) + (2.5 × 10⁻³)
- (4.5 × 10⁵) + (3.2 × 10⁷)
- (4.05 × 10⁻⁵) + (3.2 × 10⁻⁷)
- (3.5 × 10⁴) – (2.1 × 10³)
- (3.1 × 10⁻³) – (2.5 × 10⁻⁴)
- (4.5 × 10⁷) – (3.2 × 10⁵)
- (4.05 × 10⁻⁵) – (3.2 × 10⁻⁷)
Square roots using standard form
What must have been squared to give 9 × 10⁶?
Answer: we must have squared 3 to get the 9, and 10³ to get the 10⁶ (because it’s ![]() )
)
So the square root of 9 × 10⁶ is 3 × 10³.
You can check this using ordinary numbers:
3000 × 3000 = 9 000 000 ✔️
Of course, most square numbers have more than one digit.
So, for example, the square root of 16 × 10⁶ would be 4 × 10³.
But 16 × 10⁶ isn’t standard form, is it, so it probably wouldn’t be given to you in that form. Instead you’d be given it as 1.6 × 10⁷, which makes it harder to see the square root.
You’d need to turn the standard form number into a not-quite-standard form number consisting of a square number multiplied by an even power of 10. (You’ll never be given a non-calculator question of this type where that isn’t possible.)
Try it with 4.9 × 10⁹ :
The square number with those digits is 49 (which of course is 7²)
so we need to turn 4.9 × 10⁹ into
49 × 10⁸
and then it’s much easier to see that the square root is
7 × 10⁴
(or 70 000 as an ordinary number).
Your turn 3
Without using a calculator, find the square roots of these numbers, giving your answers in standard form:
- 4 × 10¹⁰
- 8.1 × 10⁵
- 3.6 × 10⁻¹¹
- 1.44 × 10¹⁰
Calculations with standard from involving algebra
At Higher Tier you will sometimes have to do algebraic calculations in standard form.
Example 1
Given that n = 3256 × ![]() , express n in standard form in terms of t.
, express n in standard form in terms of t.
We need to divide by 1000 to get the 3256 into the right range for standard form.
So we multiply the ![]() by 10³ to compensate,
by 10³ to compensate,
giving 3.256 × ![]()
= 3.256 × ![]()
Example 2
Given that![]() ,
,
find the values of p and q.
Solution:
We can write the LHS as ![]()
and this has to equal 3.5 × 10⁹
So the ![]() has to give us 3.5:
has to give us 3.5:![]()
=> q = 2
and the ![]() must be the same as 10⁹
must be the same as 10⁹
So p – 6 = 9
=> p = 15
Alternative approach:
Multiply both sides by ![]() (The denominator) to get
(The denominator) to get![]()
So 7 = 3.5q, giving q = 2
and the powers of 10 must match so p = 9 + 6 = 15.
Your turn 4 – more challenging standard form questions
Complete these calculations without using a calculator. The first two are fairly straightforward but after that you get onto the trickier algebraic ones. Full solutions are provided if you click on the link at the bottom of the exercise.

Well, there you go – that covers just about everything you’re ever likely to get thrown at you involving standard form in GCSE/IGCSE (and probably beyond).

If you’ve found this article helpful then please share it with anyone else who you think would benefit (use the social sharing buttons if you like). If you have any suggestions for improvement or other topics that you’d like to see covered, then please comment below or drop me a line using my contact form.
On my sister site at at mathscourses.co.uk you can find – among other things – a great-value suite of courses covering the entire GCSE (and Edexcel IGCSE) Foundation content, and the “Flying Start to A-level Maths” course for those who want to get top grades at GCSE and hit the ground running at A-level – please take a look!
If you’d like to be kept up to date with my new content then please sign up to my mailing list using the “Subscribe here” form at the bottom of this page, which will also give you access to my collection of free downloads.
Answers
Your turn 1 answers
- 6 × 10⁷
- 16 × 10⁸ = 1.6 × 10⁹
- 24 × 10⁻² = 2.4 × 10⁻¹
- 4.2 × 10⁴
- 1.2 × 10⁻¹¹
- 0.6 × 10¹⁰ = 6 × 10⁹
Click here to return to questions
Your turn 2 answers
- 3.71 × 10⁴
- 2.81 × 10⁻³
- 3.245 × 10⁷
- 4.082 × 10⁻⁵
- 3.29 × 10⁵
- 2.85 × 10⁻³
- 4.468 × 10⁷
- 4.018 × 10⁻⁵
Click here to return to questions
Your turn 3 answers
- 2 × 10⁵
 = 9 × 10²
= 9 × 10²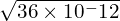 = 6 × 10⁻⁶
= 6 × 10⁻⁶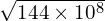 = 12 × 10⁴ = 1.2 × 10⁵
= 12 × 10⁴ = 1.2 × 10⁵
Click here to return to questions
Your turn 4 answers