Powers of 10 and Standard Form for Foundation GCSE Maths

Standard form is a way of writing very big or very small numbers without using long strings of zeroes. (It can of course also be used for more manageable numbers!) This tutorial will help you understand the meanings of different powers of 10, and teach you how to convert ordinary numbers to and from standard form.

Place value and powers of 10

To be able to work with standard form you need a good understanding of powers of 10 and the place values they represent.

Positive powers of 10

10 × 10 = 10² = 100
If we multiply 10 by 10 then we have 10 squared, which is 100: a 1 with two zeroes after it.

Similarly, 10 × 10 × 10 = 10³ = 1000 (a 1 followed by three zeroes)
and 10 × 10 × 10 × 10 = 10⁴ = 10 000 (a 1 followed by 4 zeroes)

What would 10⁶ look like if you wrote it out as an ordinary number?

Answer: a 1 followed by six zeroes, i.e. 1 000 000, one million.

The place values that you know as ones (or units), tens, hundreds, etc. can also be represented by powers of ten.

A 10 on its own is just 10¹, ten to the power of one. So we can label the place value columns like this:
the tens column has a place value of 10¹
the hundreds column has a place value of 10² (because 10² = 100)
the thousands column has a place value of 10³ (because 10³ = 1000)
the ten thousands column has a place value of 10⁴ (because 10⁴ = 10 000)

Other powers of 10

What about the other columns in the image? Looking at the pattern of the powers of 10 that we have so far, you can see that each place that we move to the left increases the power of 10 by 1, because with each step we’re multiplying by 10.

So what happens with each place you move to the right? What will the place value of the ones/units column be?

Answer: the power of 10 goes down by 1 with each place you move to the right (because with each step you’re dividing by 10). So the place value of the ones/units column will be 10⁰.

What about the places after the decimal point: tenths, hundredths, thousandths?
Again, with each place value the power of 10 goes down by 1, so:
the tenths column has a place value of 10⁻¹ (since 10⁻¹ = )
the tenths column has a place value of 10⁻² (since 10⁻² = )
the tenths column has a place value of 10⁻³ (since 10⁻³= )
… and so on.

So we have:

Converting numbers into standard form

To be in standard form, a number must be written as
a number between 1 and 10 (with a single non-zero digit before the decimal point)
multiplied by a power of 10.

So in the image above,

• the 2 in the thousands column can be expressed as 2 thousands, or 2 × 10³
• the 3 in the hundreds column can be written as 3 hundreds, or 3 × 10².
• the 5 in the ones/units column can be written as 5 ones, or 5 × 10⁰
• the 7 in the hundredths column can be written as 7 hundredths, or 7 × 10⁻²

These are simple examples of standard form.

Your turn 1

What would these numbers be in standard form?

1. 700
2. 60 000
3. 0.4
4. 0.005

Click here for the answers

The examples above each have only one significant figure. What about more complicated numbers?

Let’s take 4370 as an example. We only want one digit – the 4 – before the decimal point so the number needs to be written as 4.37 × ten to the power of something.
Since the 4 belongs in the thousands column, that’s the 10³ column
so we have 4.37 × 10³.

What about 0.097? That needs to become 9.7 × ten to the power of something, and the 9 belongs in the hundredths, or 10⁻², column,
so in standard form it’s 9.7 × 10⁻².

Your turn 2

What would these numbers be in standard form?

1. 73600
2. 21.46
3. 0.0403
4. 0.105

Click here for the answers

Of course, all the numbers that we’ve looked at so far can easily be written as ordinary numbers. But sometimes you’ll have to deal with much bigger or smaller numbers, and that’s where standard form gets more useful.

For example, can you work out what 31 200 000 000 would be in standard form?

We need to express it as 3.12 × some power of 10.
To work out the power of 10, we need to work out how many times we’d need to multiply 3.12 by 10 to get 31 200 000 000.
You can do this by counting how many places the digits would need to move to the right to turn 31 200 000 000 into 3.12.

Of course, moving all those digits would get messy, so – although in reality it’s the digits that move, not the decimal point – it’s easier to think about where the decimal point will begin and end.
The decimal point starts off at the end of the number, i.e. after the final zero. How many places would it need to move to the left to end up between the 3 and the 1?

From the image above, you can see that it needs to go ten places to the left, so the number in standard form will be
3.12 × 10¹⁰

Now let’s try it with a very small number. What would 0.000 000 059 be in standard form?

We need 5.9 × some power of 10. What power of 10 would we need to multiply 5.9 by to get 0.000 000 059? It’s a small number, less than 1, so we know it has to be a negative power.

Again, it’s easier to think about moving the decimal point than the digits. How many places to the right would it have to go?

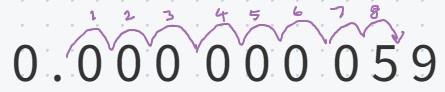
From the image above, you can see that it needs to go eight places to the right, so the number in standard form will be
5.9 × 10⁻⁸

Your turn 3

Convert these numbers into standard form:

1. 941 000 000
2. 3 205 000 000
3. 0 . 000 000 27
4. 0 . 000 010 06

Click here for the answers

Converting from standard form into ordinary numbers

Now let’s look at going the opposite way. How would you turn 5.8 × 10⁶ into an ordinary number?
Basically we take 5.8 and multiply it by 1 000 000, so the answer is 5 800 000.
The alternative way to look at it is to think about where the decimal point needs to move to in relation to the digits. It’s a positive power of 10 so it’s a big number, so the digits need to move to the left / the decimal point needs to move to the right.

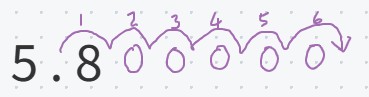
As you can see, moving the decimal point 6 places to the right gives us 5 800 000.

Now let’s try it with a small number: 4.007 × 10⁻⁵

Because it’s a negative power of 10 it must be a small number so the digits need to move to the right / the decimal point to the left, by 5 places.

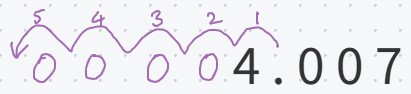
So we end up with four zeroes between the 4 and the decimal point,
i.e. the number is 0 . 000 040 07

Your turn 4

Convert these into ordinary numbers:

1. 3.6 × 10⁴
2. 7.02 × 10⁸
3. 9.1 × 10⁻⁴
4. 8.035 × 10⁻⁶

Click here for the answers

Numbers that are in not-quite-standard form

Sometimes you might be given a number that looks, as first glance, as if it’s in standard form, but in fact it isn’t, because the first part of the number doesn’t meet the criterion of having a single non-zero digit before the decimal point.

In these cases it’s likely that you’ll be asked to turn the number into standard form, so let’s look at how to do that.

Example 1: 23 × 10⁴
To turn it into standard form we need to turn the 23 into 2.3. This means that we’re dividing that part of the number by 10, so we need to multiply the other part by 10 to compensate.
When you multiply 10⁴ by 10, you get 10⁵
so 23 × 10⁴ written in standard form is 2.3 × 10⁵.

If it helps, you can turn the number you’re given into an ordinary number and then go from there to standard form, but that’s less efficient.

Example 2: 0.51 × 10⁻³
First we need to turn the 0.51 into 5.1, which means multiplying by 10. So we need to divide the 10⁻³ by 10.
Be careful – remember that when you divide by 10, the power goes down by 1, and if you go down one from -3 then that takes you to -4, not -2! So 10⁻³ ÷ 10 = 10⁻⁴
and so 0.51 × 10⁻³ written in standard form is 5.1 × 10⁻⁴.

Your turn 5

Identify which of these numbers are already in standard form, and convert the others into standard form.

1. 36 × 10⁸
2. 4.02 × 10³
3. 0.73 × 10⁵
4. 372 × 10⁴
5. 0.69 × 10⁻⁵
6. 8.01 × 10⁻⁷
7. 92 × 10⁻⁴
8. 0.024 × 10⁻⁶

Click here for the answers

Standard form on your calculator

Modern scientific calculators have a button that allows to enter numbers directly in standard form. For example, to enter 5.2 × 10⁴ you put in 5.2 then press the button, then put in the 4. When you press = or EXE, the calculator will probably display “52 000”, though it will depend on your settings.

However, if you enter a very big number then it will be left in standard form. On the calculator I’m currently using, this happens if the power of 10 you put in is 10 or greater. Negative powers also result in the number being left in standard form.

That covers standard form for Foundation GCSE up to Grade 4 standard. At the top end of Foundation, and for Higher, you also need to be able to complete calculations with numbers given in standard form; I’ll cover those in a future tutorial.

---

Answers

Your turn 1 answers

1. 7 × 10²
2. 6 × 10⁴
3. 4 × 10⁻¹
4. 5 × 10⁻³

Click here to return to questions

Your turn 2 answers

1. 7.36 × 10⁴
2. 2.146 × 10¹
3. 4.03 × 10⁻²
4. 1.05 × 10⁻¹

Click here to return to questions

Your turn 3 answers

1. 9.41 × 10⁸
2. 3.205 × 10⁹
3. 2.7 × 10⁻⁷
4. 1.006 × 10⁻⁵

Click here to return to questions

Your turn 4 answers

1. 36 000
2. 702 000 000
3. 0 . 000 91
4. 0 . 000 008 035

Click here to return to questions

Your turn 5 answers

1. 3.6 × 10⁹
2. Already in standard form
3. 7.3 × 10⁴
4. 3.72 × 10⁶
5. 6.9 × 10⁻⁶
6. Already in standard form
7. 9.2 × 10⁻³
8. 2.4 × 10⁻⁸

Click here to return to questions