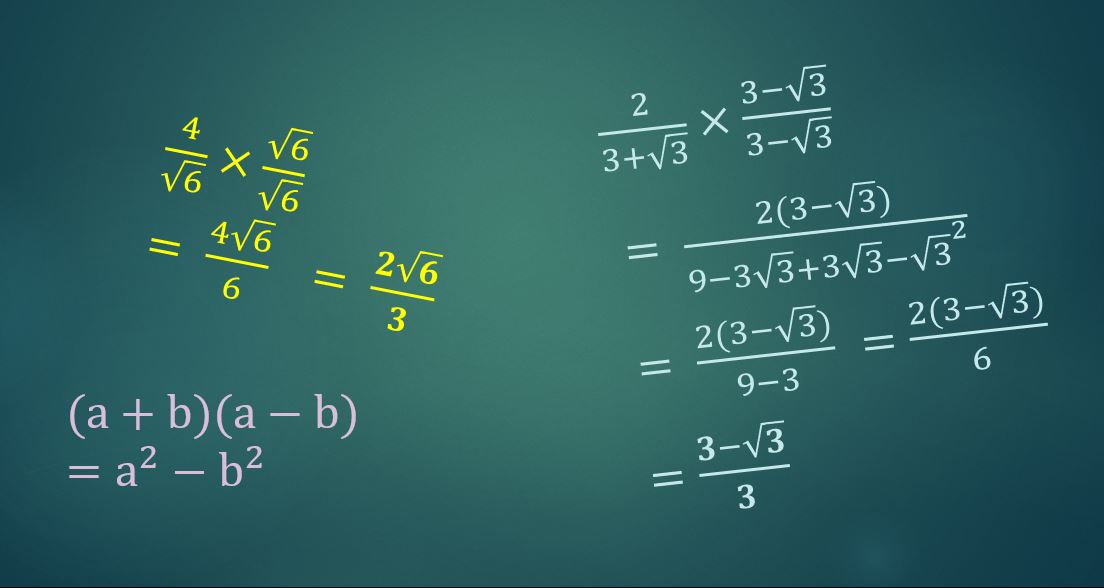This tutorial follows on from “Working with surds” and covers skills needed for Higher GCSE and beyond. If anything in this article leaves you feeling a bit lost then go back and work through the previous one first.

Rationalising the denominator

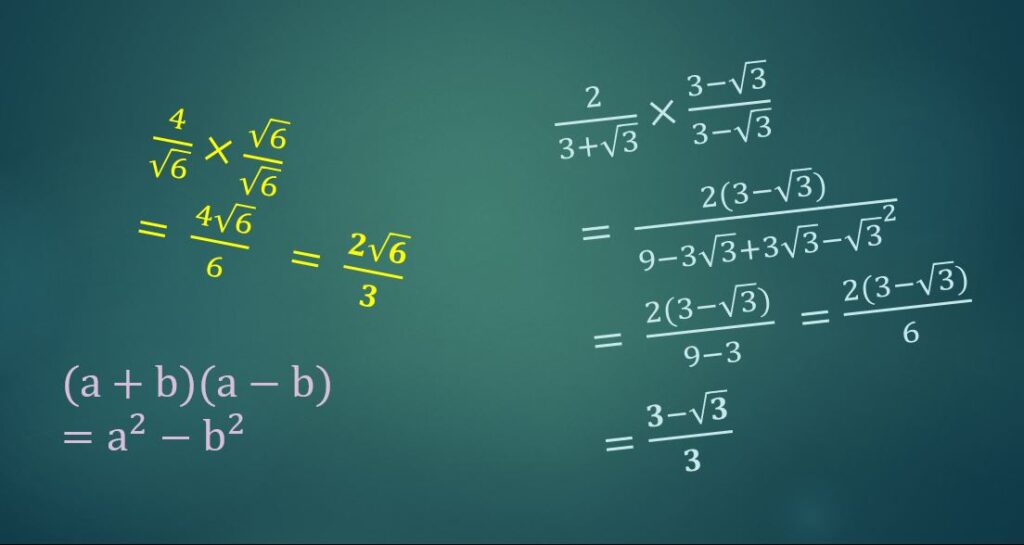
What does it mean?

We don’t like fractions with surds in the denominator. We prefer to have any surds only in the numerator. “Rationalising the denominator” means turning a fraction with one or more surds on the bottom, into an equivalent fraction with a rational denominator – normally an integer.

Simple examples

A fraction with an irrational denominator that you’ll encounter fairly frequently – for example when covering the topic on exact trig values – is $\frac{1}{\sqrt{2}}$ .

Let’s look at how to express that as an equivalent fraction without a surd on the bottom.

To make an equivalent fraction we must, of course, multiply (or divide) by the same thing both top and bottom. When deciding what that thing (number or expression) should be, we look only at the denominator and completely ignore the numerator.

What can you multiply $\sqrt{2}$ by to make a rational number?

The simplest way to do it is to multiply it by another $\sqrt{2}$ , to make 2.
So of course we also have to multiply the numerator by $\sqrt{2}$ to make an equivalent fraction:

$\frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}$

and so we now have a rational denominator.

Another example: let’s try rationalising the denominator of $\frac{6}{\sqrt{3}}$ .

To turn $\sqrt{3}$ into a rational number, multiply it by another $\sqrt{3}$ .

To make an equivalent fraction, multiply both top and bottom by $\sqrt{3}$ :

$\frac{6}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{6\sqrt{3}}{3}$ … and of course this cancels down:

$= \frac{2\sqrt{3}}{1} = 2\sqrt{3}$

Stepping it up a little

How would you go about rationalising the denominator of $\frac{2 + \sqrt{3}}{5\sqrt{3}}$ ?

Look at the denominator to decide what to multiply by: what multiplier will turn $5\sqrt{3}$ into a rational number?

You only need to multiply by $\sqrt{3}$ ; if you also multiply top and bottom by the 5 then you’ll end up having to cancel the fraction down again by a factor of 5 at the end.

So the calculation looks like this:

$\frac{2 + \sqrt{3}}{5\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{2\sqrt{3} + 3}{5 \times 3}$

$= \frac{2\sqrt{3} + 3}{15}$

(There’s no (rational) common factor here so nothing to cancel down.)

Rationalising a more complex denominator

What if you needed to rationalise the denominator of $\frac{2}{3 + \sqrt{3}}$ ?

This is where the difference of two squares, that we encountered in the previous tutorial, comes in. What do you need to multiply $3 + \sqrt{3}$ by to get a result without any surds?

Answer: $3 - \sqrt{3}$ … top and bottom, of course!

So it looks like this:

$\frac{2}{3 + \sqrt{3}} \times \frac{3 - \sqrt{3}}{3 - \sqrt{3}} = \frac{2(3 - \sqrt{3})}{9 - 3\sqrt{3} + 3\sqrt{3} - \sqrt{3}^2}$
(Note that the numerator has been left in factorised form for now; once we’ve ascertained whether the result can be cancelled down, it can be expanded, but there may be no need.)

$= \frac{2(3 - \sqrt{3})}{9 - 3}$ (since the middle terms in the denominator cancel out)

$= \frac{2(3 - \sqrt{3})}{6}$
(See, the factors of 2 on top and 6 on the bottom do cancel!)

$= \frac{3 - \sqrt{3}}{3}$

Once you get more comfortable with the $(a+b)(a - b) = a^2 - b^2$ pattern, you can skip the middle terms that you know are going to cancel out … unless it’s a “show that” question – always best to show every step on those!

For example
$(3 + \sqrt{5})(3 - \sqrt{5}) = 3^2 - \sqrt{5}^2$
$= 9 - 5$
$= 4$

Now let’s look at a more complex example:
Rationalise the denominator of $\frac{4 + \sqrt{3}}{3\sqrt{3}-5}$ .

This time we can’t use just $\sqrt{3}$ instead of $3\sqrt{3}$ , because if we do then we won’t get rid of the surds on the bottom. Try it if you like!

We need to use the “difference of two squares” approach again – the same denominator but with the opposite sign in the middle, i.e. $3\sqrt{3} + 5$ .

Try it and see how you get on, then scroll down to see the solution.
Hint: You do need to expand the brackets on the top this time, since there’s no obvious common factor that you might be able to use to cancel the fraction down later.

Solution:

$\frac{4 + \sqrt{3}}{3\sqrt{3}-5} \times \frac{3\sqrt{3}+5}{3\sqrt{3}+5} = \frac{12\sqrt{3} + 20 + 3 \times 3 + 5\sqrt{3}}{9 \times 3 + 15\sqrt{3} - 15\sqrt{3} - 25}$

$= \frac{29 + 17\sqrt{3}}{27-25}$

$= \frac{29 + 17\sqrt{3}}{2}$

Your turn

For questions 1-6, rationalise the denominator and simplify where possible:

$\frac{1}{\sqrt{7}}$
$\frac{3}{2\sqrt{3}}$
$\frac{\sqrt{2}}{\sqrt{5}}$
$\frac{6}{\sqrt{5} + 2}$
$\frac{4}{3\sqrt{3} + 5}$
$\frac{4 + \sqrt{3}}{3 + 2\sqrt{3}}$
$\frac{5 + \sqrt{3}}{4 -2\sqrt{3}}$
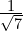
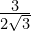
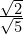
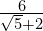
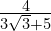
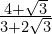
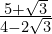
Express 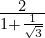$\frac{2}{1+\frac{1}{\sqrt{3}}}$ in the form $a - \sqrt{b}$ .

Click here for the answers

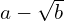That completes rationalising the denominator, which means we’ve covered all the skills you need to be able to work with surds, at both GCSE and A-level. Of course you’ll often need other skills at the same time, especially at A-level, but now you know everything you need for the surds element!

If you’ve found this article helpful then please share it with anyone else who you think would benefit (use the social sharing buttons if you like). If you have any suggestions for improvement or other topics that you’d like to see covered, then please comment below or drop me a line using my contact form.

On my sister site at at mathscourses.co.uk you can find – among other things – a great-value suite of courses covering the entire GCSE (and Edexcel IGCSE) Foundation content, and the “Flying Start to A-level Maths” course for those who want to get top grades at GCSE and hit the ground running at A-level – please take a look!

If you’d like to be kept up to date with my new content then please sign up to my mailing list using the form at the bottom of this page, which will also give you access to my collection of free downloads.

Your turn answers:

$\frac{\sqrt{7}}{7}$
$\frac{\sqrt{3}}{2}$
$\frac{\sqrt{10}}{5}$
$6\sqrt{5} - 12$
$6\sqrt{3} - 10$
$\frac{5\sqrt{3} - 6}{3}$
$\frac{13 + 5\sqrt{3}}{2}$
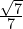
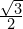
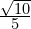
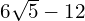
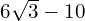
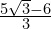
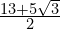
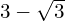$3 - \sqrt{3}$ (Hint: Start by multiplying top and bottom by 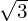$\sqrt{3}$ to get rid of the nested fraction. There are other possible approaches but this is the simplest!)