How to get the units and formula right, or basic dimensional analysis

In this tutorial you’re going to find out how, if you know the formula, you can work out what units the answer will be in, and how to use units to check whether you’ve got a formula right. It won’t tell you the whole formula, but it will tell you whether the formula you have will give you an answer in the right units!

This skill is called dimensional analysis; dimensions are essentially a fancy name for units. It’s not explicitly in the GCSE spec but it will help you to check that you’re getting things right!

Working out units

Speed, time and distance

What units do we measure distance in?

Answer: metres (or km, cm, miles, etc.)

What units do we use for time?

Answer: seconds (or hours, minutes, days, etc.)

What units do we use for speed?

Answer: metres/second … or maybe km/hour, miles/hour, cm/sec, miles/day etc.
Always [a unit of distance] ÷ [a unit of time]

So speed = distance ÷ time

Density

Can you remember the formula for density?
It’s got D, V and M in it, but in what order?

What units do we measure volume in?

Answer: m³ or cm³

What units do we measure mass in?

Answer: kg or g

Which of these are the right units for density?
kg m³?
m³/kg?
kg/m³?

If you know the formula then you’ll know that the correct units are kg/m³.

If you’re not sure of the formula but you recognise the right units then you work out which way round the formula goes.

Can you see the link?

What would the units be if we were working in cm³ and g?

More with formula triangles

If you know the speed and the time then what do you do with them to find the distance?

Multiply them: speed × time = distance

Looking at the units, we have

(The s for time is in the numerator so it cancels with the s in the denominator of m/s.)

If you are asked a question on pressure then you’ll be given the relevant formula:
Pressure = Force ÷ Area.

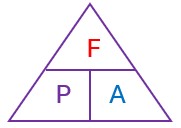
If force is measured in newtons (N) and area in m² then what will be the units for pressure?

Answer: It will be [units of force] / [units of area], i.e. N/m²

Have I got the formula right?

Formulae for area

What’s the formula for area of a rectangle?

Area of rectangle = length x width

If length and width are both in centimetres then the area will be in cm × cm = cm².

What about the area of a triangle?

Area of triangle = ½ base × height

The ½ is just a number; it has no units. So the units come from just base × height and are cm × cm = cm².

A circle?

Area of circle = πr²

π is just a number; it has no units. So the units come from just radius × radius and are, again, cm × cm = cm².

A trapezium?

Area of trapezium = ½(a + b) × h
(Half the sum of the parallel sides, times the distance between them – sing it to the tune of “Pop goes the weasel”!)

Again, ½ has no units. Adding two lengths gives another length, so the units of (a + b) are still cm. So the units here are again cm × cm = cm².

The units of area are always (a unit of length)².
To give an area, we need a formula where the only units that don’t cancel out are two lengths multiplied together.
(There could be other units but they’d have to cancel out, like the seconds did when we calculated distance by multiplying speed and time.)

Sense-checking a formula

Just as the units of area are always (a unit of length)², the units of volume are always (a unit of length)³. Therefore, to give a volume, we need a formula where the only units that don’t cancel out are three lengths multiplied together.

You CANNOT add two quantities with different units! It would be like adding pounds and dollars: you’d get a number but it would be meaningless.

If a, b, h and r are all lengths (in cm) then

• ab/h will have units (cm×cm)/cm=cm so it will give a length.
• πr² (a+b)  will have units cm² x cm = cm³ so it will give a volume.

Your turn

If a, b, h and r are all lengths (measured in metres), decide whether each of these formulae could give a length, an area or a volume, or is impossible.

1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 

Click here for the answers

So, now you know what dimensional analysis is all about and how it can help you to get your units and formulae right. I hope you’re able to make use of it!

Incidentally, if you’d like a copy of the formula sheet from which the image at the top of this page is taken (and various other downloadable freebies), take a look at this page.

---

Answers:

1. Area:
2. Volume: m³
3. Length:
4. Length:
5. Impossible: a + b² means adding m and m²
6. Area:
7. Volume: m×m² + m×m×m = m³ + m³ = m³
8. Impossible: Adding m³ and m²

Click here to return to questions