Working with iterations for GCSE Maths
In this tutorial we’re looking at iterative processes for GCSE Maths. These come in two forms at this level: trial and improvement, which is in the Foundation Tier, and working with iterative formulae, which is only required for Higher Tier.
What is iteration?
Iteration is all about coming up with a sequence of values where each value is generated from the preceding value (or values).
It’s often used to gradually home in on a solution to an equation. This can be done using trial and improvement, or using an iterative formula.
Trial and improvement
Trial and improvement means trying possible solutions and identifying a pair where one is above the actual solution and the other is below it. As long as there is no break in the graph (called an asymptote) between those two values, the actual solution must lie somewhere in that interval.
So you try another answer in between those two values, and use that to narrow down the interval, giving you an estimate that’s closer to the actual solution. Rinse and repeat until you have a solution that’s as accurate as you need.
Trial & Improvement example
Let’s look at how we can find an approximate solution for the equation![]()
Try substituting a few different values into the left side of the equation until you find two consecutive integers where one gives an value above 50 and the other gives a value below. (The TABLE function on your calculator can be useful for this, allowing you to sub in multiple different values at the same time.)
Substituting in ![]() gives
gives ![]() – too low
– too low
and ![]() gives
gives ![]() – too high
– too high
This tells us that the actual solution lies between 3 and 4 – i.e. there must be a value somewhere in that range that will give an answer of exactly 50 when you substitute it into the LHS. We can also see that 3 is well below the actual solution and 4 is just little above it, which suggests that the solution is probably closer to 4 than to 3, so it would make sense to try 3.8 or 3.9 as your next iteration. (But if you’re not sure which is closer, then it’s wise to choose a value around the middle of the interval.)
![]() gives
gives ![]() – too low
– too low![]() gives
gives ![]() – too high
– too high
This tells us that the actual solution is somewhere between 3.8 and 3.9. If we’re looking for a solution that’s accurate to 1 decimal place then all we need to do now is ascertain whether the actual solution is closer to the 3.8 or the 3.9. To do that, test the mid-point, 3.85, as a possible solution. (You MUST include this step!)
![]() gives
gives ![]() – too low
– too low
So now we know the answer is between 3.85 and 3.9, so, to 1 decimal place, the solution must be![]()
Conversely, if 3.85 had turned out to be too high then we’d know the answer was between 3.8 and 3.85, so it must be 3.8 to 1 d.p.
Here’s a model example of how to set out your answer to this question in an exam:
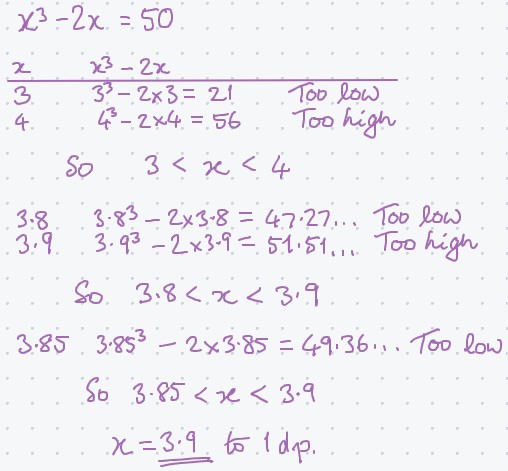
A variant of this method is the interval bisection method, where you should always use the value mid-way between the two you’ve got so far. So after 3 and 4 you’d use 3.5 for your next estimate, and 3.75 (half way between 3.5 and 4) for the one after that, and so on.
Iterative formulae
Look at the sequence 5, 8, 11, 14, 17, …
The first term, ![]() , is 5. The second,
, is 5. The second, ![]() , is 8 … and so on. You can see that each new term is formed by adding 3 to the previous one, so
, is 8 … and so on. You can see that each new term is formed by adding 3 to the previous one, so ![]()
![]()
![]()
…
and we can generalise this by using the iterative formula![]()
In other words, if we take the nth term and add 3 to it then we get the (n+1)th (i.e. next) term.
or![]()
In other words, if we want to find the nth term then we can find it by adding 3 to the (n-1)th (i.e. previous) term.
An iterative formula is also sometimes referred to as a recurrence relation, though you’re unlikely to encounter that terminology at GCSE level.
Using an iterative formula to solve an equation
Of course the example above is a very simple one. It isn’t one that will allow you to home in on the solution to an equation, but now let’s look at an example that will.
We’re going to find a solution to the same equation used in the trial and improvement example above:![]()
First we need to rearrange the equation to make one of the ![]() s the subject. We can choose either the one under the cube root sign or the one in the “
s the subject. We can choose either the one under the cube root sign or the one in the “![]() ” part. We’re going to take the former option.
” part. We’re going to take the former option.
First, get the ![]() on its own:
on its own:![]()
then cube root both sides:![]()
Now we can turn this into an iterative formula (replacing the ![]() s used earlier with
s used earlier with ![]() s) by making the “buried”
s) by making the “buried” ![]() the nth term and the isolated one the (n+1)th term:
the nth term and the isolated one the (n+1)th term:![]()
For your first term you can pick any number – not every starting point will lead you to a solution, but in an exam you’ll be told what to use as your initial estimate.
This example will use 0 but feel free to try it with other starting points. (In this case any number above -24 should do the trick.)
![]() gives
gives ![]()
then for the second iteration we plug ![]() , i.e. 3.684031, into the same formula:
, i.e. 3.684031, into the same formula:![]() gives
gives ![]()
and the third iteration:![]() gives
gives ![]()
and so on – so ![]()
So you can see that the values are converging on a solution, to 2 decimal places, of![]() .
.
Note: Not all rearrangements of the equation will result in a solution – some will give values that diverge (get further and further apart) instead of converging – but a GCSE paper will always tell you what arrangement to use. (The first part of the question could be a “Show that” asking you to rearrange the equation like we did in the example above, but giving you the form you’re aiming for.)
Handy tip: Using the Ans button for iterations
There’s a much quicker way to use an iterative formula than entering the whole thing into your calculator for each iteration: use the Ans button.
Begin by putting your start (![]() ) value into the calculator and pressing = or EXE to save it in the answer memory.
) value into the calculator and pressing = or EXE to save it in the answer memory.
Now enter the iterative formula, but wherever an ![]() appears, use Ans instead. So in this example you’ll put in
appears, use Ans instead. So in this example you’ll put in ![]()
Now press the =/EXE button and your ![]() value will be used to calculate
value will be used to calculate ![]() .
.
Press it again and ![]() , which has replaced the initial value in the answer memory, will be used to find
, which has replaced the initial value in the answer memory, will be used to find ![]() .
.
And so on! Try it starting with 0 and check that you get the same values as in the example above. Or you can start with 100000000000 if you like; you’ll take a little longer to get there but will still end up with 3.8648…
The Ans button can also be used in this way for calculations involving compound percentage change, which are another example of iteration.
Your turn
- Use trial and improvement to find a solution to 1 d.p. to the equation
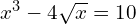 between
between  and
and 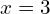 .
. - a) Show that the equation
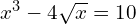 can be rearranged to
can be rearranged to ![Rendered by QuickLaTeX.com x= \sqrt[3]{4\sqrt{x} + 10}](https://b28mathstutor.co.uk/wp-content/ql-cache/quicklatex.com-57523fee0f9a816f8bb0bdf357ce3046_l3.png) .
.
b) Taking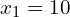 , find
, find 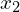 ,
, 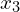 and
and 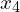 as generated by the iterative formula
as generated by the iterative formula ![Rendered by QuickLaTeX.com x_{n+1}= \sqrt[3]{4\sqrt{x_n} + 10}](https://b28mathstutor.co.uk/wp-content/ql-cache/quicklatex.com-8b946ebd5dff865b36b4dc3ee03a3364_l3.png) , recording your answers to 5 decimal places.
, recording your answers to 5 decimal places.
c) Find the solution to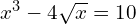 to 3 d.p.
to 3 d.p. - a) Show that the equation
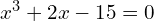 can be rearranged to
can be rearranged to 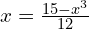 .
.
b) Use the iterative formula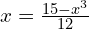 with a starting value of 2 to find a solution to the equation in (a) to 3 d.p.
with a starting value of 2 to find a solution to the equation in (a) to 3 d.p.
That covers everything you need to know about iterations for Higher GCSE.
The diagram below is a “cobweb diagram” for the equation in question 3 above, that illustrates how the iterative formula allows you to home in on the solution. You don’t need this for GCSE but will cover it when you revisit this topic if you go on to do A-level Maths.
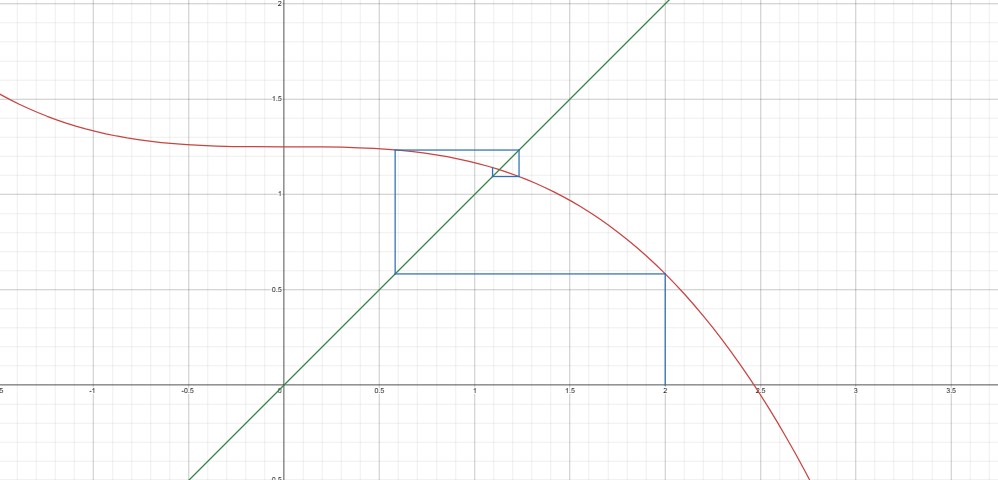
If you’ve found this article helpful then please share it with anyone else who you think would benefit (use the social sharing buttons if you like). If you have any suggestions for improvement or other topics that you’d like to see covered, then please comment below or drop me a line using my contact form.
On my sister site at at mathscourses.co.uk you can find – among other things – a great-value suite of courses covering the entire GCSE (and Edexcel IGCSE) Foundation content, and the “Flying Start to A-level Maths” course for those who want to get top grades at GCSE and hit the ground running at A-level – please take a look!
If you’d like to be kept up to date with my new content then please sign up to my mailing list using the form at the bottom of this page, which will also give you access to my collection of free downloads.
Answers:
1. Model solution:

2. a) ![]()
![]()
![]()
b) ![]()
c) ![]()
3. a) ![]()
![]()
![]()
b) ![]()
